25型基準機の冷却パターン

「スケールアップ理論を考えてみよう ー 冷却編【25型乳化撹拌装置（基準機）の冷却パターン①】」のページで紹介した話の続きとなります。

それでは，冷却パターンを25型基準機に当てはめてみましょう。

すると，下表の結果が得られました。

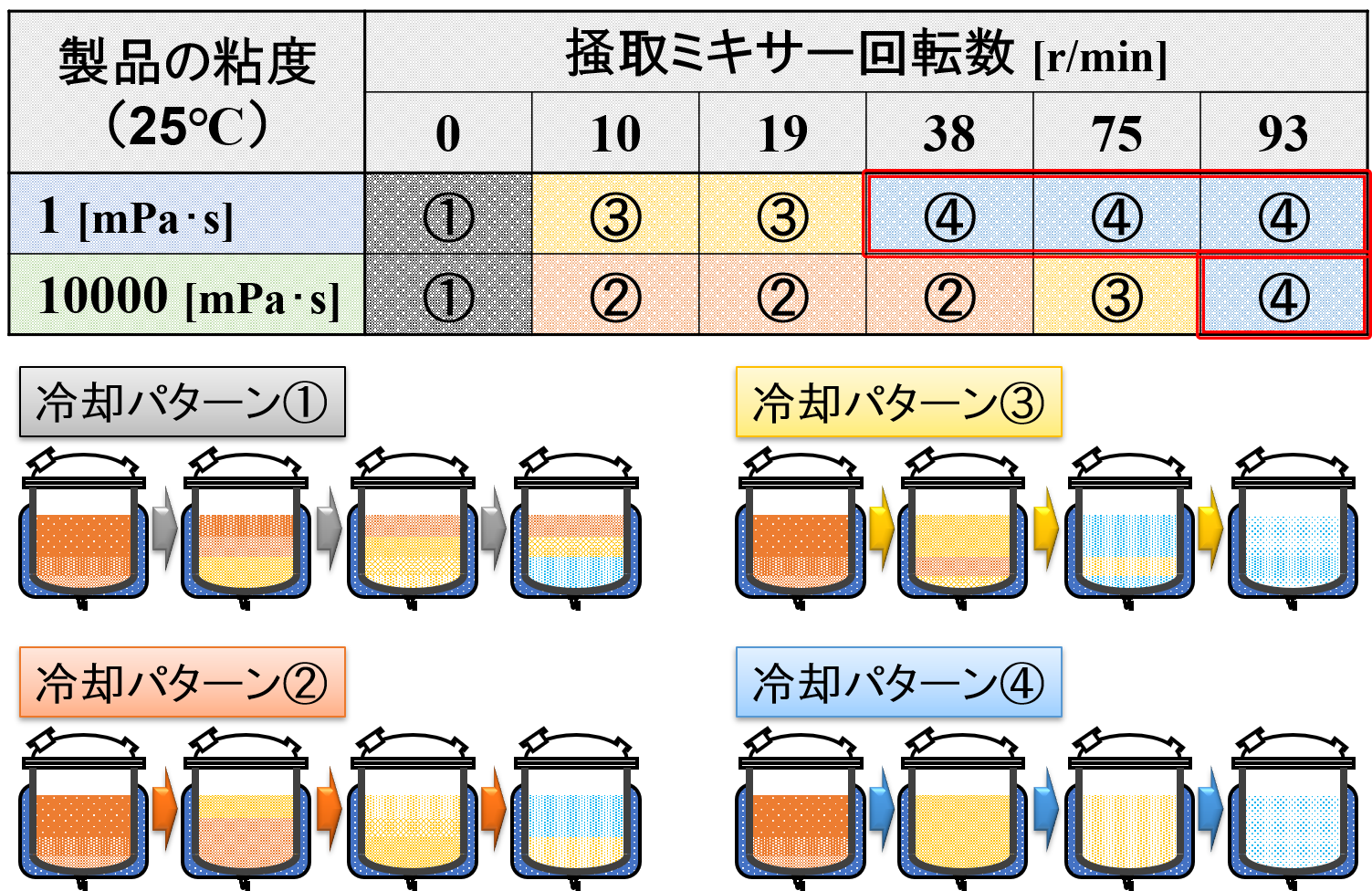
容易に予想できることですが，掻取ミキサーの回転数を高くしていくと冷却速度が速くなり，製品全体が均一に冷却されるようになります。（パターン④）

さらに，粘度が高い製品では冷却パターン④に達するまでに回転数を高くせざるを得ないことがわかります。

一方で，一度パターン④に達すると，これ以上均一な冷却は見込めません。

したがって，冷却速度が劇的に変化しない限り，さらに掻取ミキサーの回転数を高くしても意味がないかもしれません。

冷却に適切な回転数は，理論的に算出することが難しいことを説明してきました。

そのため，実際の試作結果や経験・ノウハウから導き出すことになるのが現状です。

📝[memo]　今回の事例において，1 [mPa・s]製品の場合は38 [r/min]，10000 [mPa・s]製品の場合は93 [r/min]が最適な掻取ミキサーの回転数と判断することができます。

総括伝熱係数と冷却時間

「スケールアップ理論を考えてみよう ー 冷却編【冷却時間の計算式（生産性の計算式）】」のページで，Batch Coolingの式を紹介しました。

掻取ミキサーを使用して冷却することを踏まえて，少し振り返ってみたいと思います。

冷却時間を決定する因子はいろいろありますが，乳化撹拌装置の冷却条件と製品の物性に分けて考えます。

このとき，Batch Coolingの式中の変数に注目します。

乳化撹拌装置の冷却条件

設備

• 冷却水入口温度t₁
• 冷却水量ω
• 冷却水の比熱c₂
• 乳化槽の伝熱面積A

撹拌（掻取ミキサー）

• 回転数N

撹拌（掻取ミキサー）の項で記載している回転数N以外の変数は，Batch Coolingの式に含まれています。

そのため，これらが変化すると冷却時間θが変化します。

一方で，回転数NはBatch Coolingの式に含まれていません。

そのため，回転数Nが変化しても冷却時間θが変化しないことになってしまいます。

そこで，回転数Nの変化に伴って総括伝熱係数Uも変化すると考えることで，冷却時間θが変化するようになります。

📝[memo]　実は，総括伝熱係数Uは回転数Nの関数であるという理解ですね。

製品の物性

製品

• 製品の比熱c₁
• 密度ρ
• 粘度η

製品の比熱c₁はBatch Coolingの式に含まれているので，これが変化すると冷却時間θが変化します。

一方で，密度ρと粘度ηはBatch Coolingの式に含まれていません。

そこで，密度ρと粘度ηの変化に伴って総括伝熱係数Uも変化すると考えると，冷却時間θが変化するようになります。

📝[memo]　同じく，総括伝熱係数Uは密度ρと粘度ηの関数でもあるという理解ですね。

総括伝熱係数

実験で冷却時間θがわかっているので，逆算して総括伝熱係数Uを求めると下表になります。

ここでは同じ製品で掻取ミキサーの回転数を変えているだけなので，上述した”製品の物性”は変化しないと考えて無視することにします。

すなわち，総括伝熱係数Uは回転数Nのみの影響を受けるとして解釈します。

📝[memo]　総括伝熱係数Uは，従来Dにおける温度を考えています。

ここで，1 [mPa・s]製品の場合を考えてみましょう。

このとき，冷却パターン④に達する38 [r/min]が最適であると判断しました。

さらに掻取ミキサーの回転数Nを高くすると，総括伝熱係数Uが大きくなっているので冷却時間θが短縮されていることがわかります。（321 → 349 → 362）

ただし，この冷却時間θの短縮が意味を持つ結果であるか否かの検証が必要です。

冷却時間θが大きく短縮されない限り，掻取ミキサーの回転数Nを高くするのは避けた方が良いと言えます。

冷却工程に不必要な微細化作用が発揮されるため，製品の物性を変化させてしまうかもしれません。

総括伝熱係数と冷却時間

話の内容としては，撹拌機メーカー寄りの余談となります。

読み飛ばしていただいて問題ありません。

理論的な検討ではあるのですが，応用事例ですね。

「スケールアップ理論を考えてみよう ー 冷却編【冷却速度一定とする考え方①】」のページで，ジャケット冷却による係数β₁を紹介しました。

単位体積あたりの槽壁伝熱量の式で登場する因子であり，撹拌羽根が同じであれば一定の値となります。

冷却時において，温度によってエマルション製品の密度ρや粘度ηが連続的に変化するという問題がありましたが，これらが一定であると仮定します。

📝[memo]　現状とそぐわないかもしれませんが，一旦このように仮定します。

すると，総括伝熱係数Uを使用することでジャケット冷却による係数β₁を求めることができます。

ジャケット冷却による係数の算出

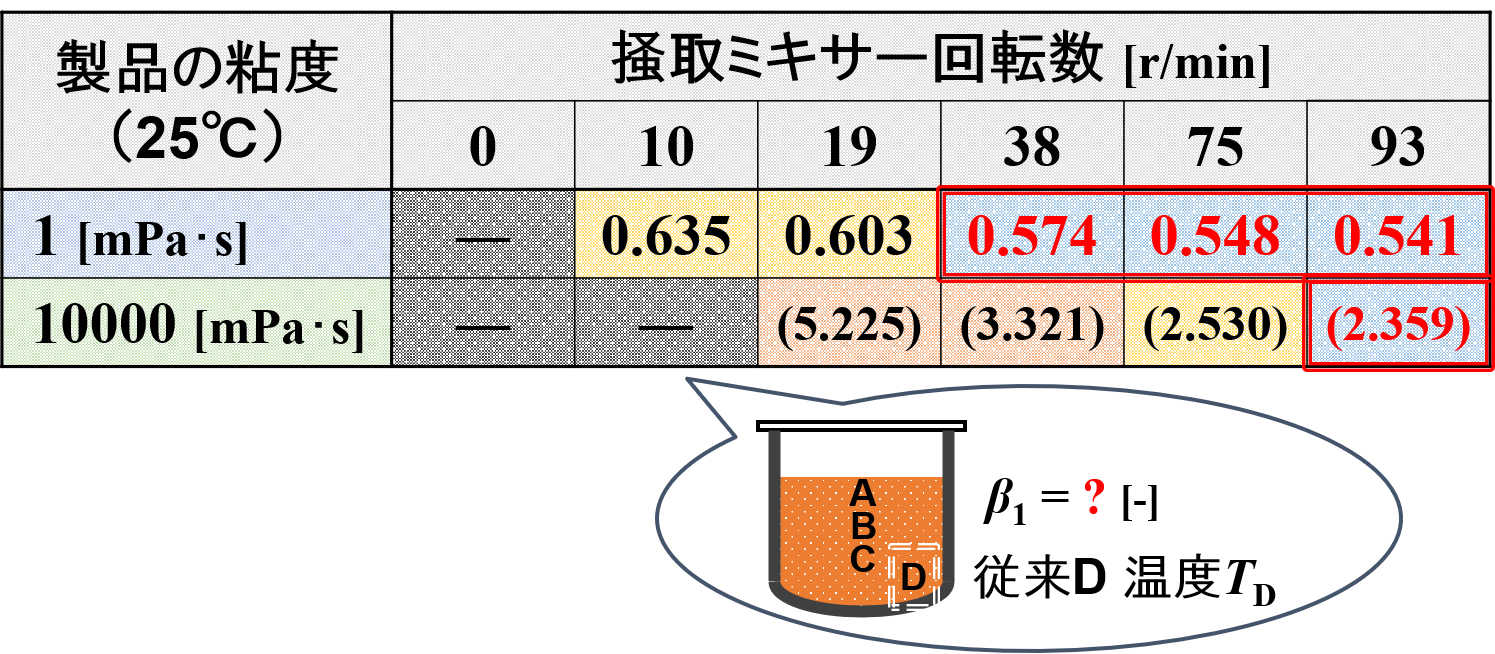
上述した考えに基づいて計算すると，下表の結果が得られます。

ただし，乱流域で使用できる考え方であるため，10000 [mPa・s]製品の場合は層流域となるため結果は参考値です。

データ数は少ないですが，ジャケット冷却による係数β₁は0.54 ~ 0.58程度となることがわかります。

これが，掻取ミキサーを使用した冷却能力を示す1つの指標となります。

他の撹拌羽根も同じように評価できそうですね。

次に，文献値と比較をしてみましょう。

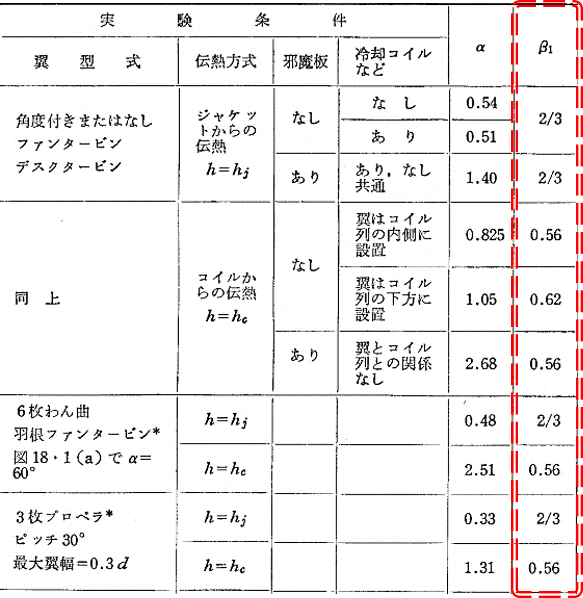
下図は，各種撹拌羽根におけるジャケット冷却による係数を抜粋したものです。

結果として，文献値と近い値が得られました。

この結果が正しいのであれば，掻取ミキサーは従来の撹拌羽根と似たような性能と言うことができます。

これからは，ジャケット冷却による係数が大きくなった新規撹拌羽根の開発や既存の掻取ミキサーの最適な使用方法の選定等，さらなる技術向上が望まれるところです。

📝[memo]　まずはお試しの計算をやってみましたが，掻取ミキサーの働きと製品の冷却現象について当社で検討を続けています。

🚩 [引用：社団法人化学工学協会編『化学工学便覧』丸善，1988]

ジャケット冷却による係数β₁の導出

最後に，ジャケット冷却による係数β₁を導出するまでの流れを紹介したいと思います。

ここまで余談が続きましたが，これで終わりとします。

① 単位時間あたりの伝熱量　q = U・ΔT・A
② 単位体積あたりの槽壁伝熱量　q_V = q/V = Reβ₁/D²・ΔT ⇔ q = VReβ₁/D²・ΔT
③ 撹拌レイノルズ数　Re = ND²ρ/60η

①②は等しいので，

U・ΔT・A = VReβ₁/D²・ΔT ⇔ U・A = VReβ₁/D²

⇔ Reβ₁ = UAD²/V ⇔ β₁lnRe = ln(UAD²/V)

β₁ = ln(UAD²/V)/lnRe

このようにして，ジャケット冷却による係数β₁が得られます。