このページの注意❕

このページは計算式が登場したりと，少し深く踏み込んだ内容でやや複雑となっています。

抽象的な話が続くので大変かもしれません。

難しいなと思われた方は…，

次ページ「撹拌の立場から乳化をイメージしよう【ギブス自由エネルギーのイメージ①】」へ迷わず移動しましょう！

ここでの内容は，粒子化して小さくなると界面の影響を大きく受けるので，通常では起こりえない現象が生じるかもしれませんよ！と説明しています。

応用的な話が続くので，読み飛ばしていただいても問題ありません。

界面自由エネルギーの式を使ってみる

「撹拌の立場から乳化をイメージしよう【界面自由エネルギーの考え方】」のページの続きとなります。

”界面自由エネルギーの式”というものが出てきました。

雰囲気を掴んでいただくことはできたでしょうか？

ここでは，界面自由エネルギーの式を使って大きな液滴と小さな液滴を比較することで，界面自由エネルギーの意味について少し掘り下げていくことにしましょう。

界面自由エネルギーと液滴の大きさ

ここまで，界面自由エネルギーの式を使って「液滴の体積に対する界面自由エネルギーの割合」というものを計算をしてみました。

文字を使った表現と計算式が出てくるようになりますが，次のような大きな液滴と小さな液滴が存在していると仮定して比較をしてみましょう。

大きな液滴の場合

仮に，次で示す大きな液滴が存在するとして考えることにします。

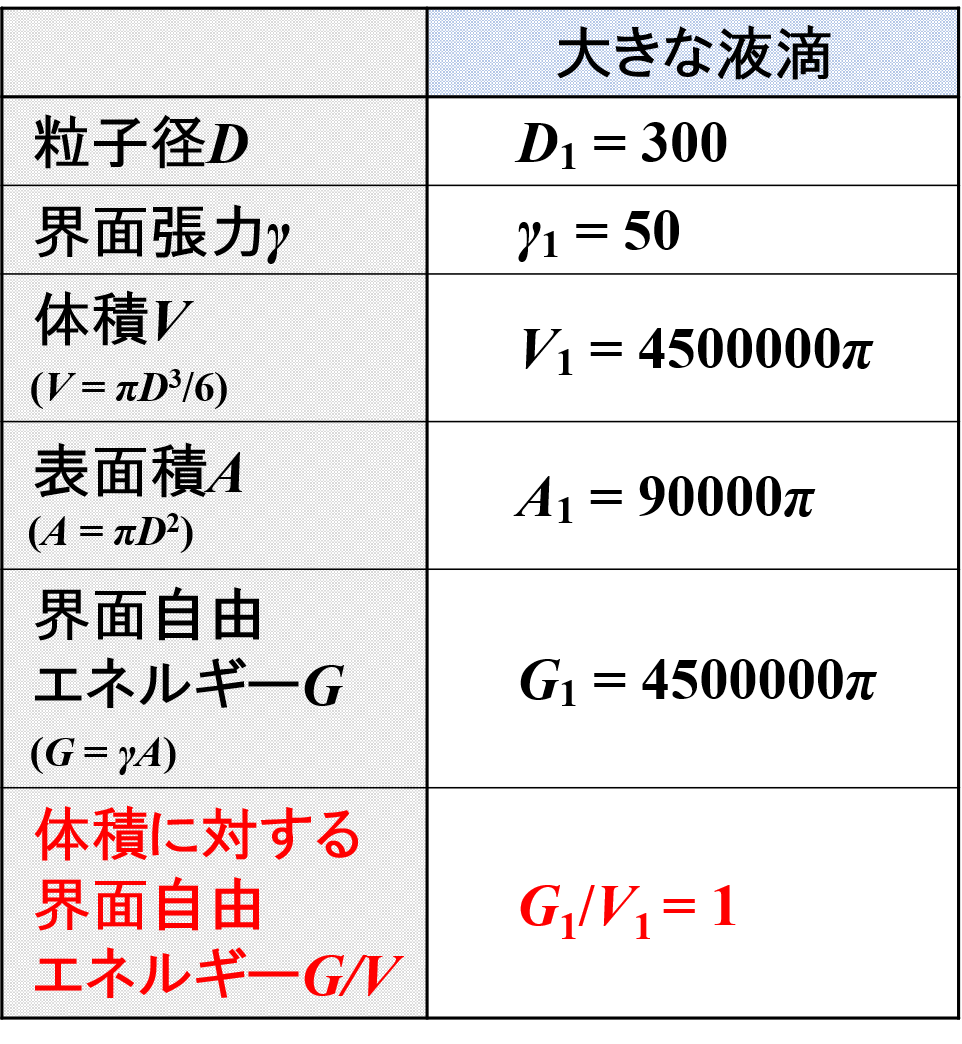
大きな液滴の大きさ（粒子径）D₁，界面張力γ₁

大きな液滴の大きさ（粒子径）は「D₁ = 300」，その界面張力は「γ₁ = 50」であったとします。

大きな液滴の体積V₁，表面積A₁，界面自由エネルギーG₁

次に，大きな液滴の体積V₁，表面積A₁，界面自由エネルギーG₁について，各種公式から算出することにします。

その結果，下表の通りとなります。

ここで，大きな液滴の体積に対する界面自由エネルギーの割合というものを考えることにします。

これを計算すると，「G₁/V₁ = 4500000π/4500000π = 1」となります。

…ということは，大きな液滴の表面には，その体積に対して1倍の界面自由エネルギーが蓄えられていることがわかりました。

よくわからない結論だと思いますが，このような結果が得られたとして小さな液滴についても同様に考えてみましょう。

小さな液滴の場合

仮に，次で示す小さな液滴が存在するとして考えることにします。

小さな液滴の大きさ（粒子径）D₂，界面張力γ₂

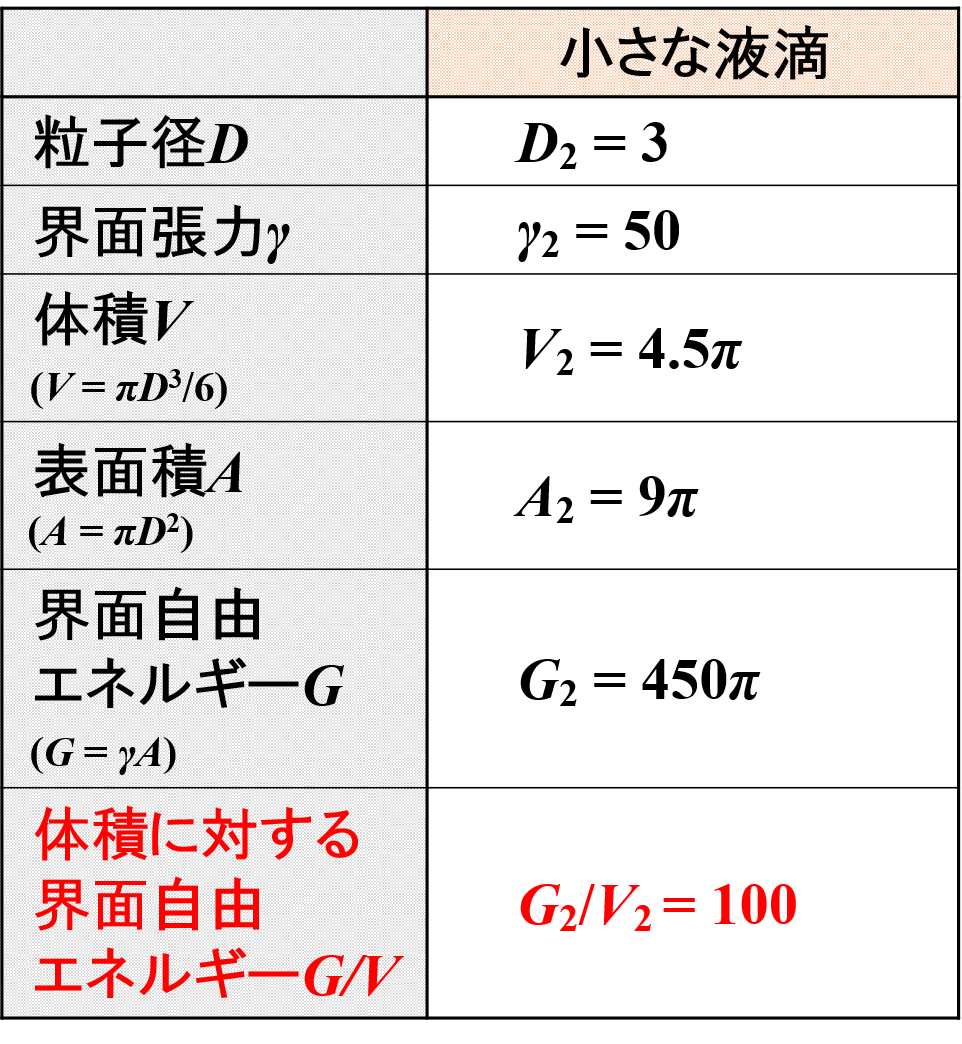
小さな液滴の大きさ（粒子径）は「D₂ = 3」，その界面張力は「γ₂ = 50」であったとします。

📝[memo]　小さな液滴は，大きな液滴の1/100の大きさ（D₂ = 1/100×D₁）であると仮定します。

📝[memo]　液滴を構成する成分は同じであるため，界面張力は変化しない（γ₂ = γ₁）とします。

小さな液滴の体積V₂，表面積A₂，界面自由エネルギーG₂

大きな液滴のときと同様に，小さな液滴の体積V₂，表面積A₂，界面自由エネルギーG₂について各種公式から算出すると，下表の通りとなります。

このとき，小さな液滴の体積に対する界面自由エネルギーの割合は「G₂/V₂ = 450π/4.5π = 100」となります。

…ということは，小さな液滴の表面には，その体積に対して100倍の界面自由エネルギーが蓄えられていることがわかりました。

どうやら，大きな液滴とは異なる結果になるようです。

界面自由エネルギーに関する計算結果のまとめ

液滴の体積に対する界面自由エネルギーの割合を計算すると，大きな液滴と小さな液滴とで差が生じることがわかりました。

• 大きな液滴の体積に対する界面自由エネルギーの割合は「G₁/V₁ = 1」
• 小さな液滴の体積に対する界面自由エネルギーの割合は「G₂/V₂ = 100」

粒子径が1/100倍になると，液滴の体積に対する界面自由エネルギーの割合は100倍になります。

📝[memo]　「G₂/V₂ = 100G₁/V₁」となります。

それでは，この結果をどのように解釈したら良いでしょうか？

界面自由エネルギーの解釈

ここまで，界面自由エネルギーの式を使って試しに計算をしてみました。

その結果，大きな液滴と小さな液滴の間には違いがあることがわかりました。

そこで，次のような解釈をしてみましょう。

液滴を作るためには外部エネルギーが必要

初期状態から粒子化するとき，界面の表面積が大きくなります。

そのため，「”界面”を作ることができるだけのエネルギー」が必要になります。

このときのエネルギーを”界面自由エネルギー”としたわけです。

したがって，界面自由エネルギーに相当する外部エネルギーが必要であることがわかります。

…ということは，どのような大きさの液滴を作る場合であっても，必ず外部エネルギーを付与しなければならないことを意味します。

「撹拌の立場から乳化をイメージしよう【エマルションの調製手順と機械的な力】」のページでも触れ，外部エネルギーを撹拌と捉え考えることにします。

ここまで，「液滴の体積に対する界面自由エネルギーの割合」というものを曖昧にしてきましたが，ある大きさの液滴を形成するために必要なエネルギーと解釈できそうです。

• 大きな液滴の体積に対する界面自由エネルギーの割合は「G₁/V₁ = 1」
• 小さな液滴の体積に対する界面自由エネルギーの割合は「G₂/V₂ = 100」

このような結果から，大きな液滴より小さな液滴を形成する方が，より多くの界面自由エネルギー＝外部エネルギーが必要であることがわかります。

小さな液滴を形成するためには大きな外部エネルギーが必要ですよ！という結論なので，これまでのイメージ通りで理解しやすい結果になったと思います。

界面自由エネルギーが物性を変化させる

外部エネルギーを付与することによって，大きな液滴と小さな液滴が形成したと仮定しましょう。

そうすると，それぞれの液滴の表面には，界面自由エネルギーが蓄えられていると考えることができます。

そして，蓄えられている界面自由エネルギーが過剰であったとします。

界面自由エネルギーは「”界面”を作るために使われる」と解釈しましたが，このエネルギーの一部が”界面”を作る以外の用途にも使われる可能性もあります。

小さな液滴の体積に対する界面自由エネルギーの割合が「G₂/V₂ = 100」であることから，大きな液滴（G₁/V₁ = 1）よりも界面自由エネルギーの影響は大きいと考えることができます。

液滴の体積に対する界面自由エネルギーの割合が大きいということは，言葉通り，液滴の成分が界面自由エネルギーの影響を大きく受けることを意味しています。

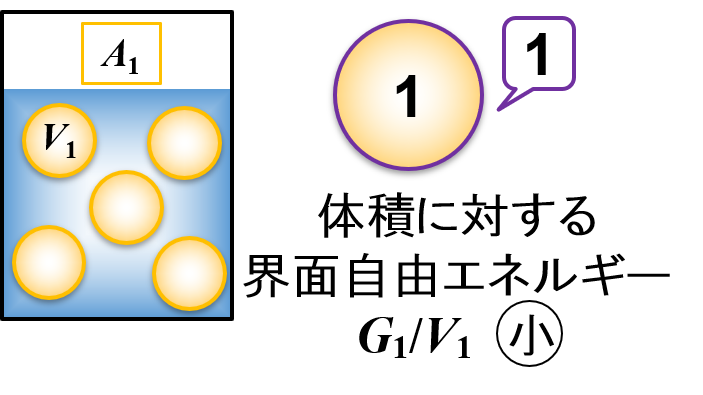
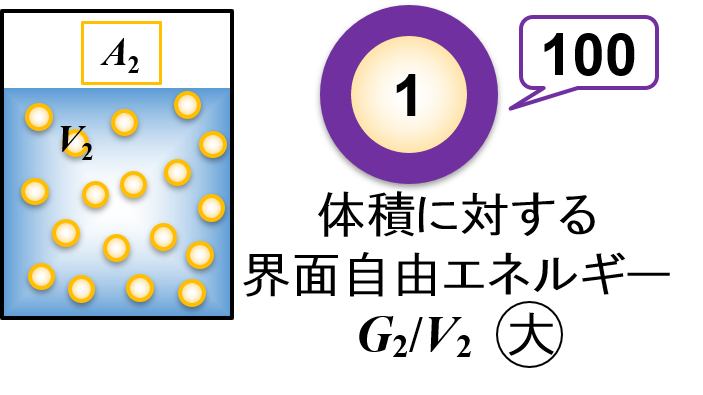
すなわち，微粒子化して小さな液滴を作ると，液滴の成分が持つ基本的な物性を変化させる可能性が高まります。

📝[memo]　白金の融点は1700 [℃]以上ですが，白金ナノ粒子にすることによって数100 [℃]まで融点が下がる（＝物性変化）ことが知られています。

こうした理由から，ナノ粒子と呼ばれる非常に小さな液滴を生成させ，新たな物性を見出す試みがなされています。

📝[memo]　エマルションを安定化する目的もあります。

📝[memo]　 詳しくは「スケールアップでエマルションを評価しよう【エマルションの安定性（クリーミング）】」のページで紹介することにします。