分析機器

「スケールアップでエマルションを評価しよう【スケールアップ成否の評価方法】」のページにおいて，各製品に応じた評価方法が決められていないのであれば，スケールアップの成否の判定は，粒子径および粒度分布の評価によって行うことができるとの結論を見出しました。

ここでは，分析機器を用いて，エマルションの粒子径および粒度分布測定をすることを考えます。

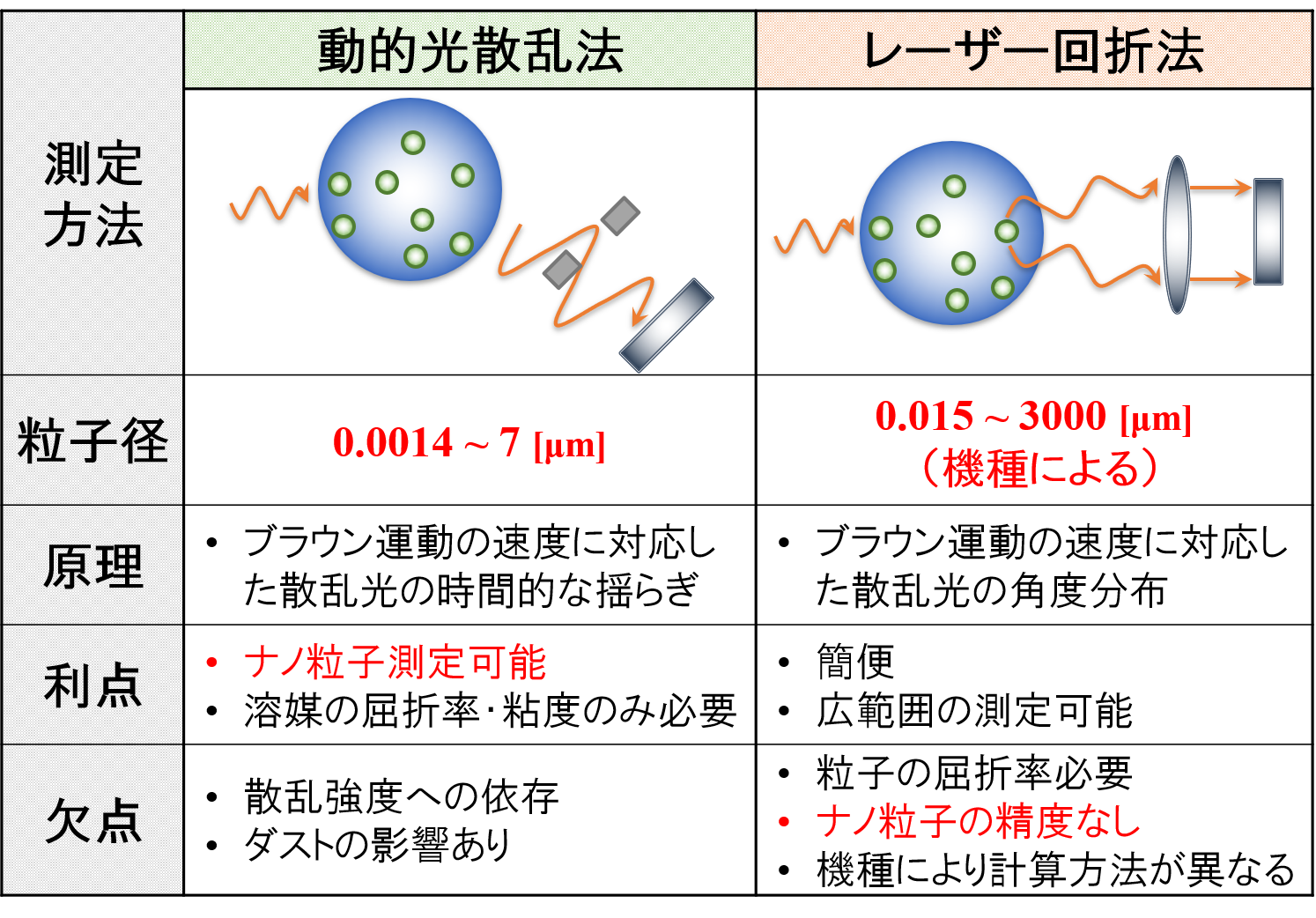
粒子径及び粒度分布測定の原理・特徴

分析機器においては，様々な測定方法が採用されています。

下図は，代表的な測定方法の概要を示したものです。

詳細な説明は分析機器メーカーにお任せしますが，エマルション中の乳化粒子がブラウン運動で動くとき，そのときの速度を粒子径として換算しているイメージです。

分析機器メーカーによって異なりますが，一般に，乳化粒子の大きさによって測定方法（分析機器）を使い分ける必要があります。

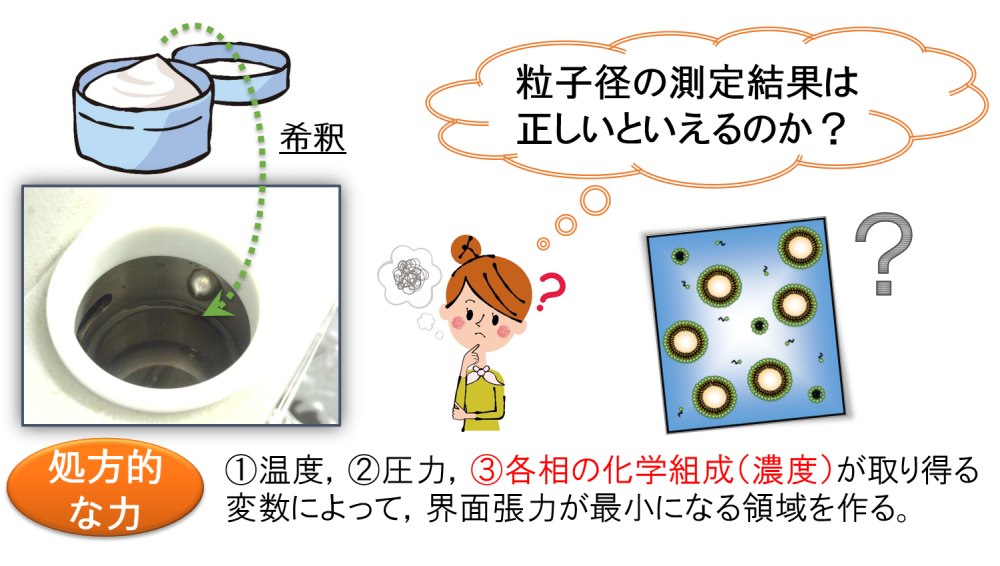
測定時におけるエマルションの希釈

次に，実際に測定する手順について考えてみましょう。

実は，測定に最適な散乱強度を得るために，エマルションを水で希釈しないといけません。

📝[memo]　動的光散乱法やレーザー回折法のいずれの手法であっても，このような事情があります。

ここで，”処方的な力”について今一度考えてみます。

最適条件となるように「③各相の化学組成（濃度）」を決定しました。

しかしながら，測定時にエマルションを水で希釈するので「③各相の化学組成（濃度）」が変化します。

…ということは，元々のエマルション製品の物性が変化してしまうことを意味します。

そのため，分析機器によって得られる「粒子径の測定結果は正しいといえるのか？」という疑問点が付きまといます。

したがって，暗黙のうちに下記のような仮定がなされていることになります。

エマルションを水で希釈したとしても，乳化粒子径は一切変化しないと仮定する。

👉　測定で得られた値は，正しいものとして信用する。

エマルションを水で希釈すると，乳化粒子径はある一定の割合で変化すると仮定する。

👉　測定で得られた値は，その大小を比較するときのみに使用する。

📝[memo]　本来であれば，エマルションを水で希釈せずに粒子径を直接測定をしたいものです。

測定によって得られるデータ

例えば，分析機器を用いてエマルションの粒子径および粒度分布測定をすると，下図のような結果がデータシートとして得られます。

ここでは， データシート に記載されている重要な語句4つをピックアップします。

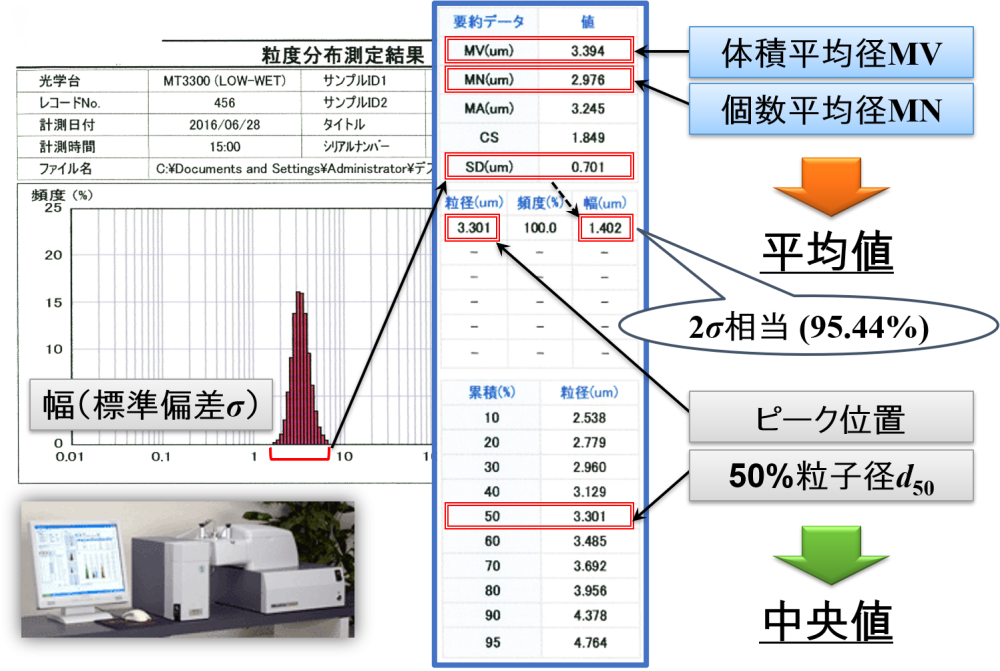
• 体積平均径MV　👉　平均値
• 個数平均径MN　👉　平均値
• 50%粒子径d₅₀　👉　中央値
• 幅σ　👉　標準偏差

少なくともこれらの意味を知っておくと，エマルション中で引き起こされている現象を考察する際，乳化粒子の状態を想像するのに役に立ちます。

「スケールアップ理論を考えてみよう ー 乳化編【エマルションの粒子径とその粒度分布解析】」のページで，考察の例を紹介しています。

ここでは，これらの数学的な意味合いから捉えることにしましょう。

📝[memo]　ピーク位置の考え方は中央値に基づいていると言えるので，1つの粒子集団のみが存在するときはそのピーク位置は50%粒子径d₅₀と一致します。

📝[memo]　明らかに区別できる複数の粒子集団が存在するとき，例えば粒子集団を2つに区別できるときは2つのピーク位置が得られますが，50%粒子径d₅₀とは一致しません。

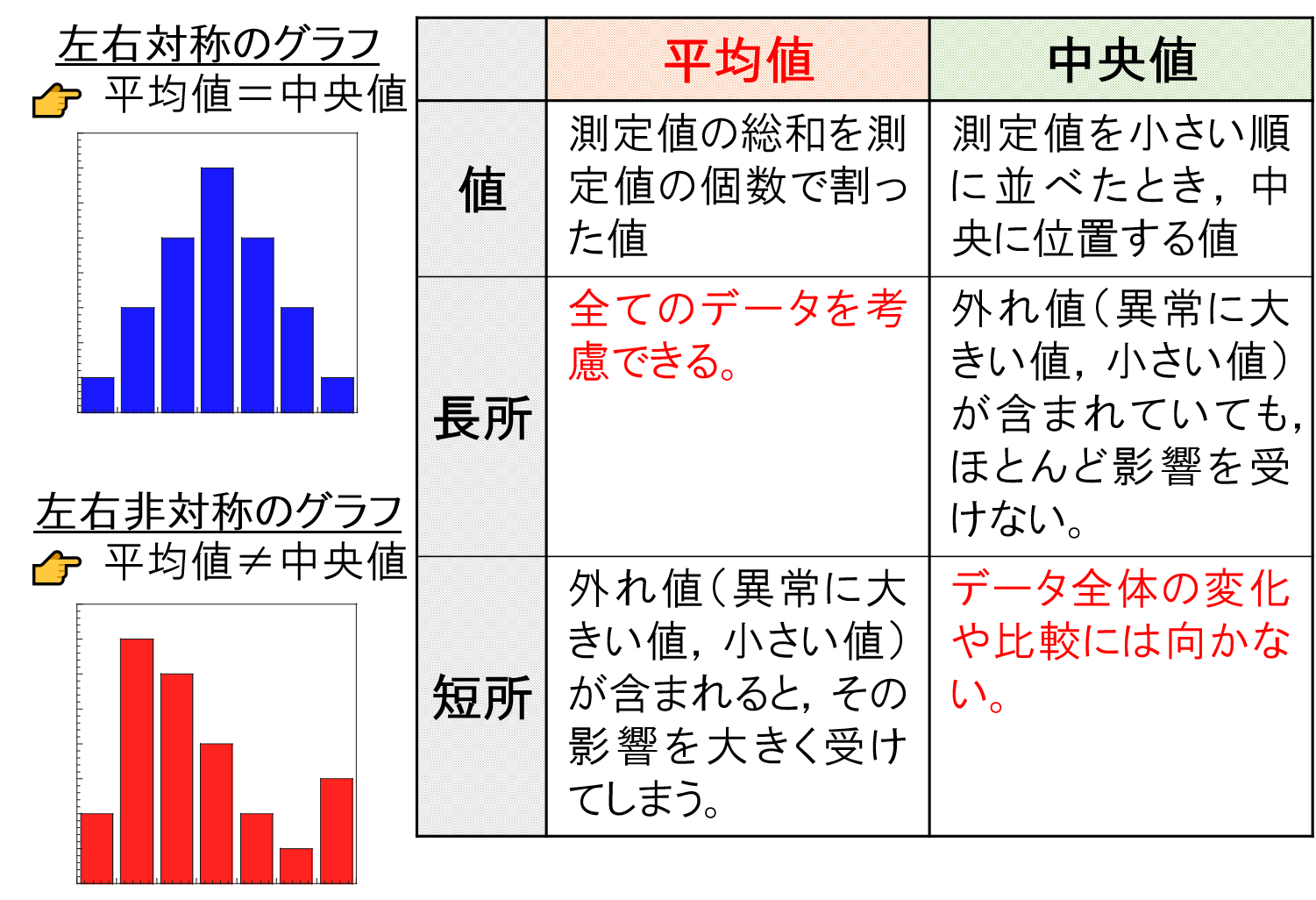
平均値や中央値とは…

体積平均径MVと個数平均径MNは平均値，50%粒子径d₅₀は中央値による粒子径を示しています。

”平均値”はどのような特徴があったでしょうか？

ご存知の通り，平均値とは測定値の総和を測定値の個数で割った値のことです。

…ということは全てのデータを考慮できるので，これが最大の長所と言えます。

一方，外れ値（異常に大きい値，小さい値）が含まれるとその影響を大きく受けてしまうので，これが一般的に短所であると言われています。

一方で，分析をする以上，異常があれば測定結果としてすぐに反映して欲しいところです。

そのため，今回の目的においては，ここで言う一般的な短所（異常に大きい値，小さい値が含まれるとその影響を大きく受けてしまうこと）を長所とみなすことができます。

次に，”中央値”はどのような特徴があったでしょうか？

中央値とは測定値を小さい順に並べたとき，中央に位置する値のことです。

…ということは外れ値（異常に大きい値，小さい値）が含まれていてもほとんど影響を受けないので，これが一般的に最大の長所と言えます。

上述したように，分析をする以上，異常があれば測定結果としてすぐに反映して欲しいところです。

したがって，データ全体の変化や比較には向かないという短所があります。

このように考えると，スケールアップ時における評価として，”平均値”に該当する粒子径を採用するのが良さそうです。

📝[memo]　絶対に，中央値を使用してはいけないという意味ではありません。あくまでも1つの考え方です。

📝[memo]　横軸を粒子径としたとき，左右対称のグラフの場合は「平均値＝中央値」となります。

標準偏差とは…

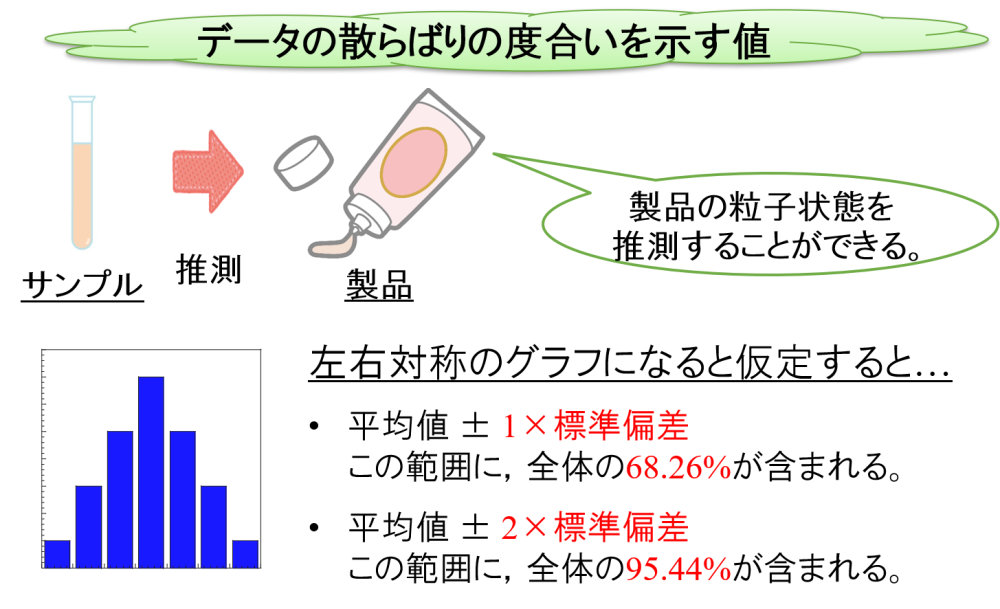
標準偏差を一言で言うと，データの散らばりの度合いを示す値ということになります。

標準偏差が小さいほうが，平均値からのばらつきが小さいと言えます。

ここで，ガラスのコップの重さを調べることを考えたいと思います。

例えば，はかりでその重さを調べたところ，「131.54 [g]」と表示されたとします。

このとき，我々はガラスのコップの重さは「131.54 [g]」であると認識します。

当たり前の話ですが，ガラスのコップの重さとして「131.54 [g] ± 10.0 [g]（121.54 [g ] ~ 141.54 [g]）」のような認識はしません。

必ず，特定の値「131.54 [g]」であると理解します。

一方，粒子径及び粒度分布測定においては特定の値としておらず，幅を持つ”標準偏差”の考え方が採用されています。

これは，なぜでしょうか？

全体測定と部分測定

ガラスのコップの重さは，その全量（全てのガラスが集まったもの）を計測しています。

一部のガラスを計測して，コップの重さを推測していません。

一方，粒子径及び粒度分布測定では，エマルション全体を一部のサンプルのみから評価しています。

したがって，一部のサンプルからエマルション全体の状態を推測する必要があります。

…すると，本来であれば特定の値としたいところですが，測定値（推測値）は幅が必要となります。

このような事情が，”標準偏差”の考え方を採用している理由と言えそうですね。

エマルションは分散液

「撹拌の立場から乳化をイメージしよう【水溶液と分散液】」にて，エマルションは分散液であることを説明しました。

すなわち，乳化粒子の大きさが不均一であるので，エマルション全体を一部のサンプルのみから評価して特定の値とすること自体が困難です。

…ということで，上述した内容と同じ結論になりますが，”標準偏差”の考え方が採用されている理由と言えそうですね。

ちなみに，標準偏差は次のような意味を持ちます。

標準偏差が小さいほうが，平均値からのばらつきが小さいと言えることに変わりありません。

平均値 ± 1×標準偏差

エマルションに含まれる全粒子の大きさのうち，この範囲に68.26%が含まれます。

• 20 [μm] ± 1×1 [μm]　👉　19 [μm] ~ 21 [μm]　全体の68.26%がこの粒子径の範囲（ばらつきが小さい）
• 20 [μm] ± 1×5 [μm]　👉　15 [μm] ~ 25 [μm]　全体の68.26%がこの粒子径の範囲（ばらつきが大きい）

平均値 ± 2×標準偏差

エマルションに含まれる全粒子の大きさのうち，この範囲に95.44%が含まれます。

• 20 [μm] ± 2×1 [μm]　👉　18 [μm] ~ 22 [μm]　全体の95.44%がこの粒子径の範囲（ばらつきが小さい）
• 20 [μm] ± 2×5 [μm]　👉　10 [μm] ~ 30 [μm]　全体の95.44%がこの粒子径の範囲（ばらつきが大きい）

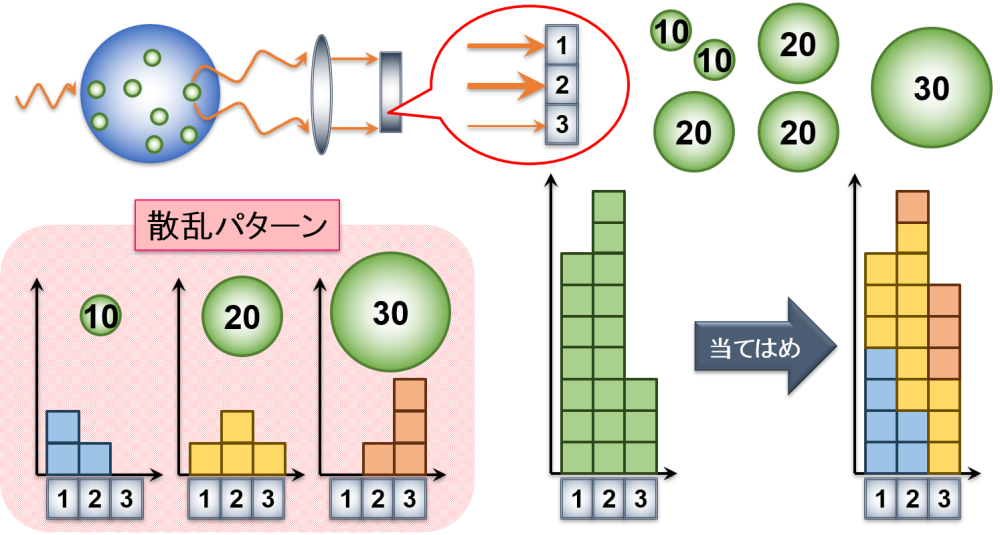
レーザー回折法における粒度分布への変換

最後に，少しだけ測定原理のイメージを紹介をします。

粒子の大きさによってレーザー光の散乱パターンが決まっていて，これを当てはめることをします。

例えば，検出器1~3で得られる大きさ10, 20, 30の粒子の散乱パターンが下図の通りであったとします。

あるエマルションを測定したとき，検出器1では強度7，検出器2では強度9，検出器3では強度6が得られたとします。

すると，大きさ10の粒子：2個，大きさ20の粒子：3個，大きさ30の粒子：1個を含むエマルションであると推測することができます。