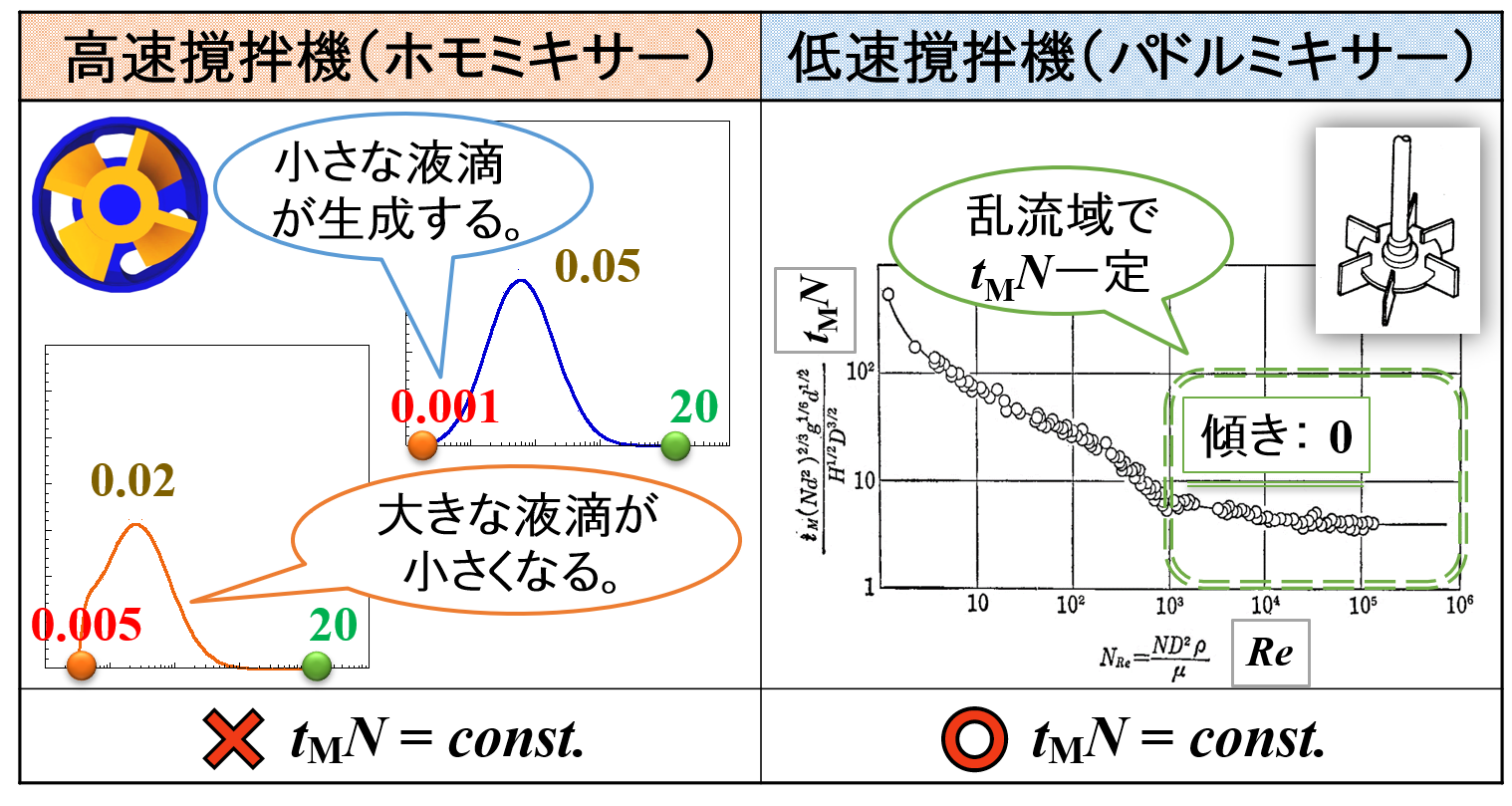
回転数と乳化/混合時間の関係

ここで，高速撹拌機（ホモミキサー）と低速撹拌機（パドルミキサー）の比較をしてみましょう。

ポイントは，「スケールアップ理論を考えてみようー乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介した無次元混合時間の考え方（混合時間と回転数の積が一定）が，高速撹拌機に対して適用できるか否かということです。

高速撹拌機によって液滴が分裂していくモデルを考え，回転数と乳化時間に対する粒子径の変化を考えてきましたが，乳化時間と回転数の積が一定とはなりそうにありません。

高速撹拌機では，最適な回転数と乳化時間がそれぞれ存在します。

ただ，無次元混合時間のように，回転数と乳化時間の間には何らかの関係性はあるかもしれません。

したがって，無次元混合時間の考え方は，高速撹拌機を使用した液滴の分裂モデルにはそのまま採用できないことがわかります。

乳化粒子（液滴）が小さくなっていくとき

「スケールアップでエマルションを評価しよう【粒子径および粒度分布解析②】」のページで，様々な粒子径が意味することを紹介しました。

そして，「スケールアップでエマルションを評価しよう【エマルション製品に対する考察例】」のページで評価をすることをしましたが，あくまでもスケールアップの立場から粒子径を考えていたかと思います。

一方，「スケールアップ理論を考えてみよう ー 乳化編【高速撹拌機による液滴の微細化】」のページで，回転数や乳化時間が変化することによって，液滴の粒子径がどのように変化するかについて紹介しました。

ここでは，乳化粒子が小さくなっていくとき，粒度分布解析の視点からどのようなことが起こり得るかを考えたいと思います。

ピーク位置（ピークトップ）

ピーク位置の考え方は中央値に基づいていると言えるので，1つの粒子集団のみが存在するときはそのピーク位置は50%粒子径d₅₀と一致します。

明らかに区別できる複数の粒子集団が存在するとき，例えば粒子集団を2つに区別できるときは2つのピーク位置が得られますが，50%粒子径d₅₀とは一致しません。

したがって，明らかに区別できる複数の粒子集団が存在するか否かを判断するために使用することが多いです。

個数平均径 MN

個数平均径MNは粒子数が強く反映されると考えることができます。

大きな液滴が分裂して小さな液滴が生成するとき，当然ながら粒子径は小さくなりますが，併せて生成する粒子の数も増加します。

このとき，回転数（せん断力）が一定で個数平均径MNが経時変化しないのであれば，最終的に調製できる乳化粒子の大きさの目安になります。

📝[memo]　液滴が分裂を起こす最小せん断応力が決まっていましたよね。

体積平均径 MV

体積平均径MVは占める体積が強く反映されると考えることができます。

大きな乳化粒子があったとき，すぐに粒子径として反映します。

もし，全ての乳化粒子が同じように微細化されるのであれば，MV = MNとなります。

したがって，乳化粒子のばらつき具合の目安になり，乳化時間を長くすることで乳化粒子のばらつきを解消することが期待できます。

📝[memo]　ピーク位置を示す粒度分布の見た目や，標準偏差からも同様の評価をすることができます。

様々な液滴の微細化モデルと粒子径（粒度分布解析）

乳化粒子が小さくなると言っても，様々な粒子径変化が考えられます。

初期の状態では大きさ20の液滴が存在しており，これを微細化することを考えます。

ここでは，以下に示すモデルケースについて，粒度分布解析の視点から考察したいと思います。

📝[memo]　50%粒子径d₅₀，個数平均径MN，体積平均径MVを中心に考えます。

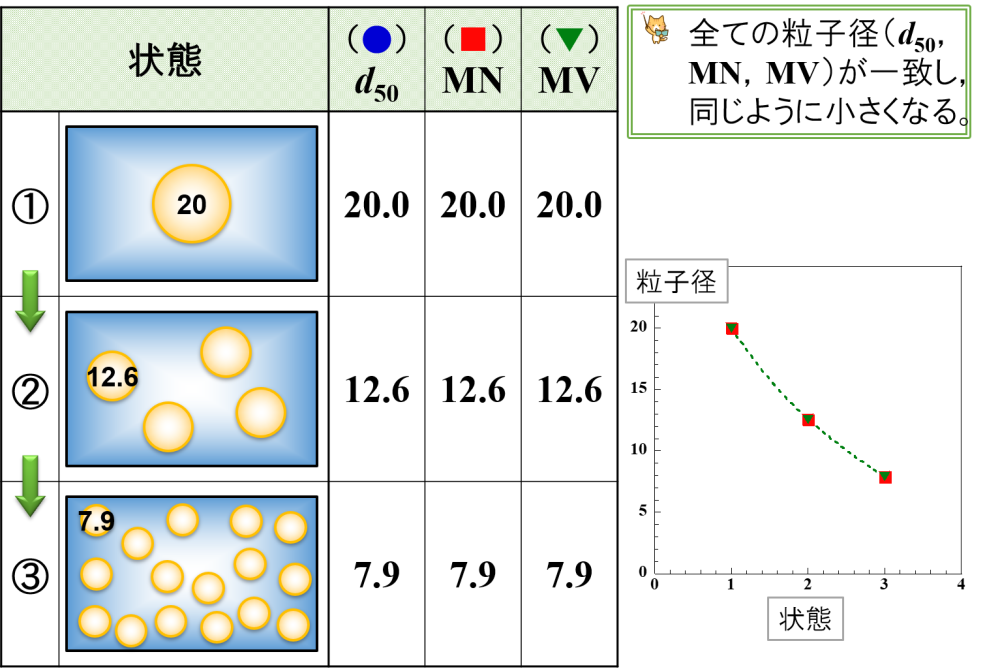
⑴ 全ての乳化粒子が同じように微細化

液滴が微細化されて，常に同じ大きさの液滴が存在するような変化です。

全ての粒子径（d₅₀, MN, MV）が一致し，同じように小さくなります。

📝[memo]　全ての粒子径がほぼ一致する程度であっても，理想的な状態と言えます。

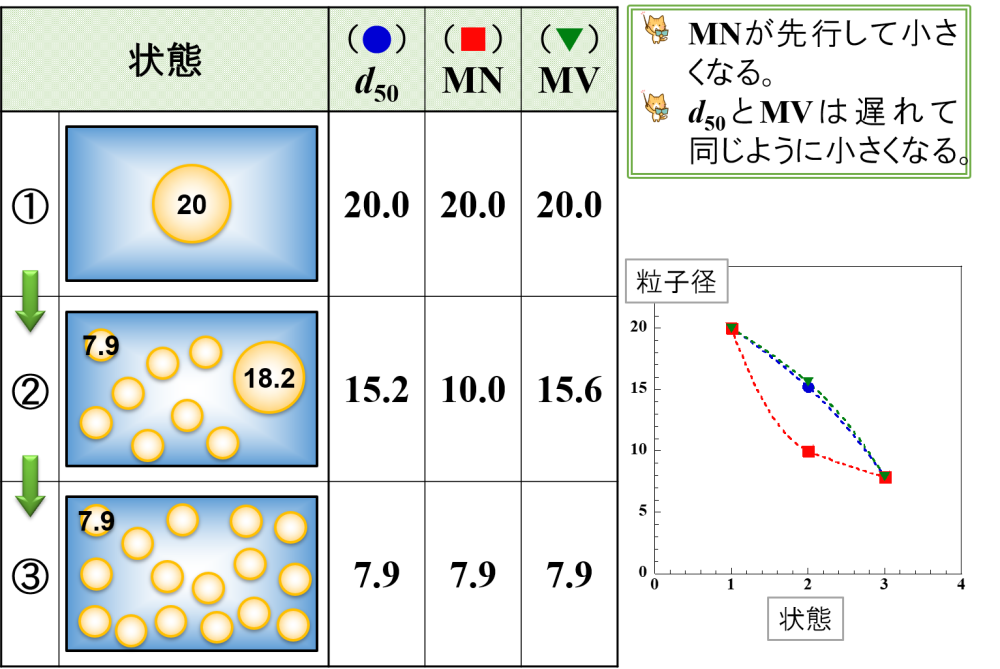
⑵ 全ての乳化粒子が順番に微細化

⑴と似たような変化ですが，先に液滴が微細化されて小さな液滴が生成し，続いて大きな液滴が微細化されるパターンです。

小さな液滴が生成するので，MNが先行して小さくなります。

そして，d₅₀とMVは遅れて同じように小さくなります。

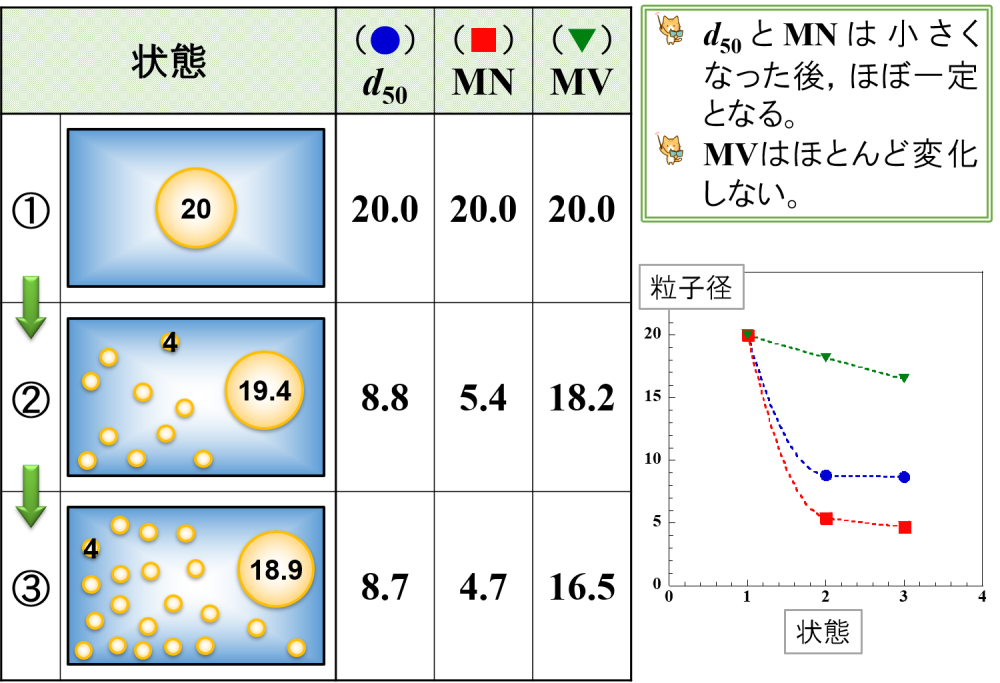
⑶ 大きな乳化粒子の一部が微細化①

大きさ20の液滴が微細化されて，大きさ4の小さな液滴が生成し続けるパターンです。

早い段階で小さな液滴が生成するので，d₅₀とMNは小さくなった後，ほぼ一定となります。

📝[memo]　最終粒子径に近いと判断することができます。

大きさ20の液滴は微細化されますが，大きな液滴として残り続けます。

そのため，MVはほとんど変化しないと言えます。

尚，状態②③では大きさ4と大きさ19.4または18.9の粒子集団に区別されるため，ピーク位置が2つ検出される可能性があります。

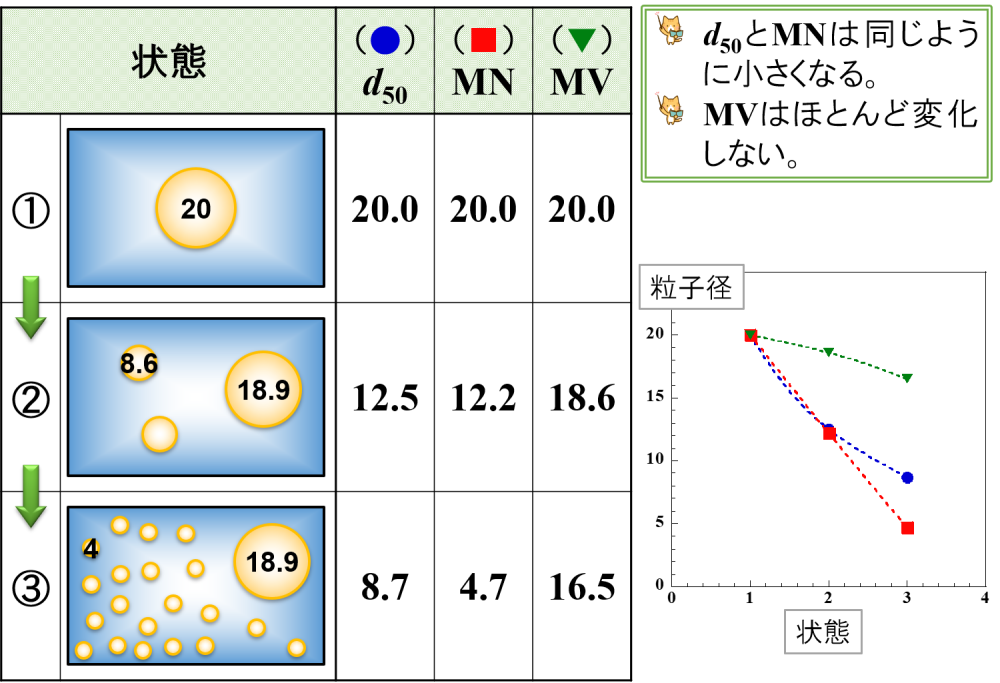
⑷ 大きな乳化粒子の一部が微細化②

⑶と似たような変化ですが，大きさ20の液滴が微細化されて大きさ8.6となり，さらに微細化されて大きさ4の小さな液滴が生成するパターンです。

だんだんと小さな液滴が生成していくので，d₅₀とMNは同じように（徐々に）小さくなります。

大きさ20の液滴は微細化されますが，大きな液滴として残り続けます。

そのため，MVはほとんど変化しないと言えます。

尚，状態③では大きさ4と大きさ18.9の粒子集団に区別されるため，ピーク位置が2つ検出される可能性があります。

📝[memo]　状態②では大きさ8.6と大きさ18.9の粒子集団に区別されるのであれば2つのピーク，同じ粒子集団と判断されれば1つのピークとなります。

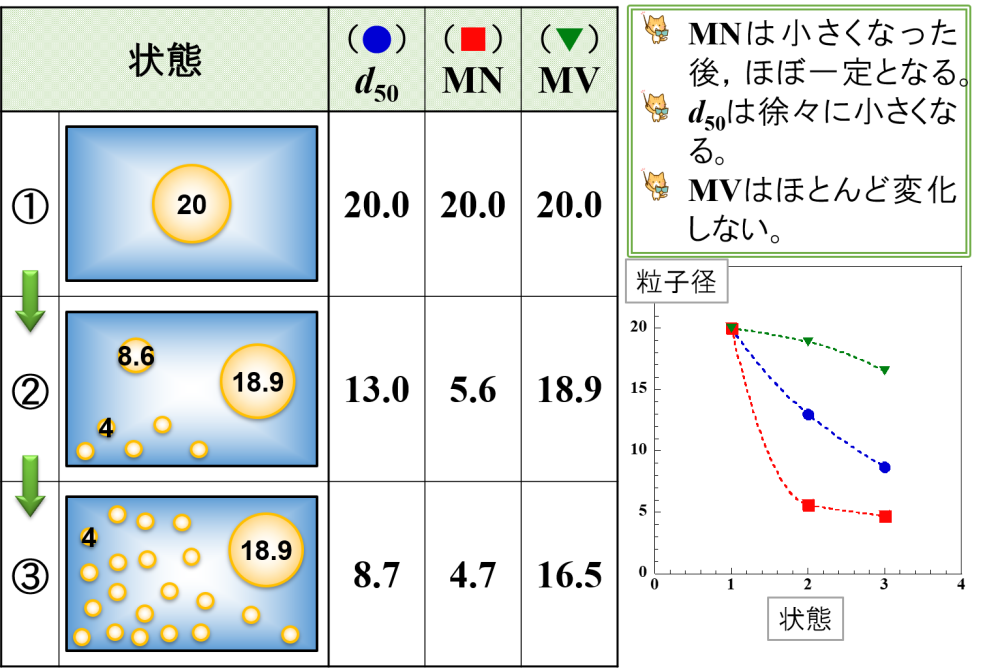
⑸ 大きな乳化粒子の一部が微細化③

⑶と⑷を混ぜたような変化ですが，大きさ20の液滴が微細化されて大きさ8.6若しくは4となります。

大きさ8.6の液滴は，さらに微細化されて大きさ4の小さな液滴が生成するパターンです。

早い段階で小さな液滴が生成するので，MNは小さくなった後，ほぼ一定となります。

また，だんだんと小さな液滴が生成していくので，d₅₀は徐々に小さくなります。

大きさ20の液滴は微細化されますが，大きな液滴として残り続けます。

そのため，MVはほとんど変化しないと言えます。

尚，状態③では大きさ4と大きさ18.9の粒子集団に区別されるため，ピーク位置が2つ検出される可能性があります。

📝[memo]　状態②では大きさ4，8.6，18.9の液滴を含むブロードなピークになると考えられます。

撹拌条件と粒子径の関係

ここで，一旦整理をしておきましょう。

「スケールアップ理論を考えてみよう ー 乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介したように，回転数が高くなると付与するせん断力が大きくくなります。

また，乳化時間が長くなると，パス回数が増えます。

“最終粒子径”到達前と後

「スケールアップ理論を考えてみよう ー 乳化編【高速撹拌機による液滴の微細化】」のページで紹介したように，“最終粒子径”到達前であれば，回転数を高くしたり乳化時間を長くすると，乳化粒子全体の粒子径が小さくなると言えます。

その結果，小さな液滴は一番数が多くなるので個数平均径MN，大きな液滴はその体積も大きいので体積平均径MVが小さくなると理解できます。

次に，“最終粒子径”到達後になったときを考えます。

さらに回転数が高くなると付与するせん断力が大きくなるので，小さな液滴がさらに小さくなる傾向が見られます。（同時に大きな液滴も小さくなります）

同様にしてさらに乳化時間が長くなるとパス回数が増えるので，大きな液滴のみが小さくなり，液滴の粒度分布が均一になる傾向が見られます。

📝[memo]　表中の関係式はこれから出てくる内容なので，ここでは一旦無視しておきましょう。

分裂確率と粒子径

このように考えると，回転数を高くして大きなせん断力を付与するほど，等分数が大きくなって「最小粒子」＝「個数平均径MN」が小さくなることがわかります。

📝[memo]　等分数は，「スケールアップ理論を考えてみよう ー 乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介しました。

逆に言うと，個数平均径MNが小さくなることは大きなせん断力が付与されていることを意味します。

基本的にはこのように考えれば良いのですが，一部例外があります。

それは，分裂確率が大きく異なるときです。

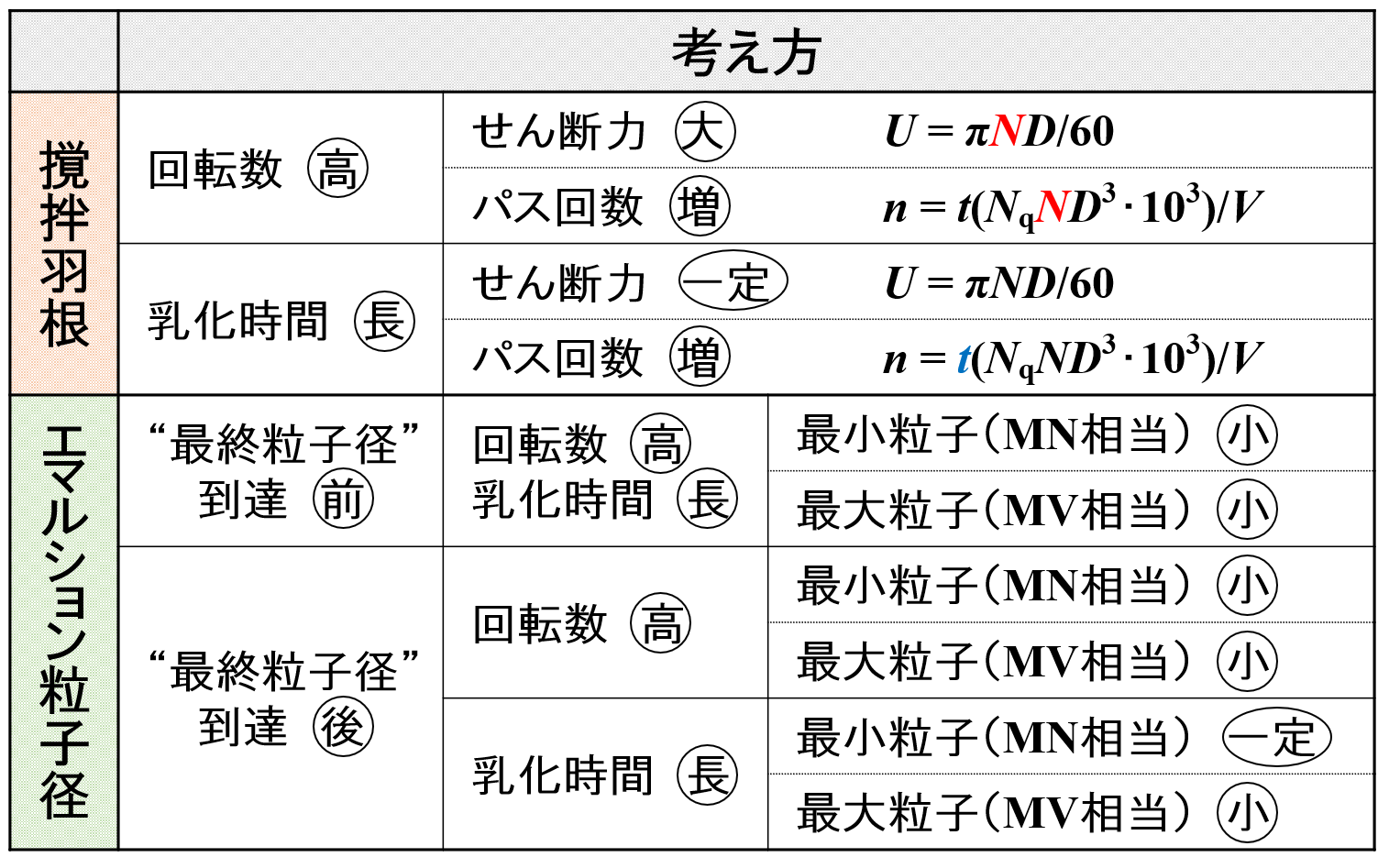
例えば24回分裂するチャンスがあったとき，分裂確率が60%と20%の場合を考えます。

最初の粒子の大きさを20と仮定し，等分数の違いによる粒子径の分布を確認してみましょう。

📝[memo]　個数平均径MNの前に，粒度分布（ピークトップ）を調べます。

いずれの分裂確率の場合であっても，回転数を高くして大きなせん断力を付与する（等分数を大きくする）と，確かに小さな粒子が存在していることがわかります。

しかしながら，このような小さな粒子の存在よりも，ピークトップに注目が集まると思います。

📝[memo]　実際の分析装置においても，ピークトップを粒子径として表したものが多いと思います。

そこで，下図の等分数3（●）と等分数5（□）を比較すると等分数3（●）のときの方がピークトップが小さくなっており，これまでに説明してきたことと矛盾しているように見えます。

これは，等分数が小さくても分裂確率が高いので，粒子が小さくなりやすいと言えます。

このように，付与するせん断力（等分数）が小さくても，分裂確率が高ければ粒子径ピークトップが小さくなることがあり得るということです。

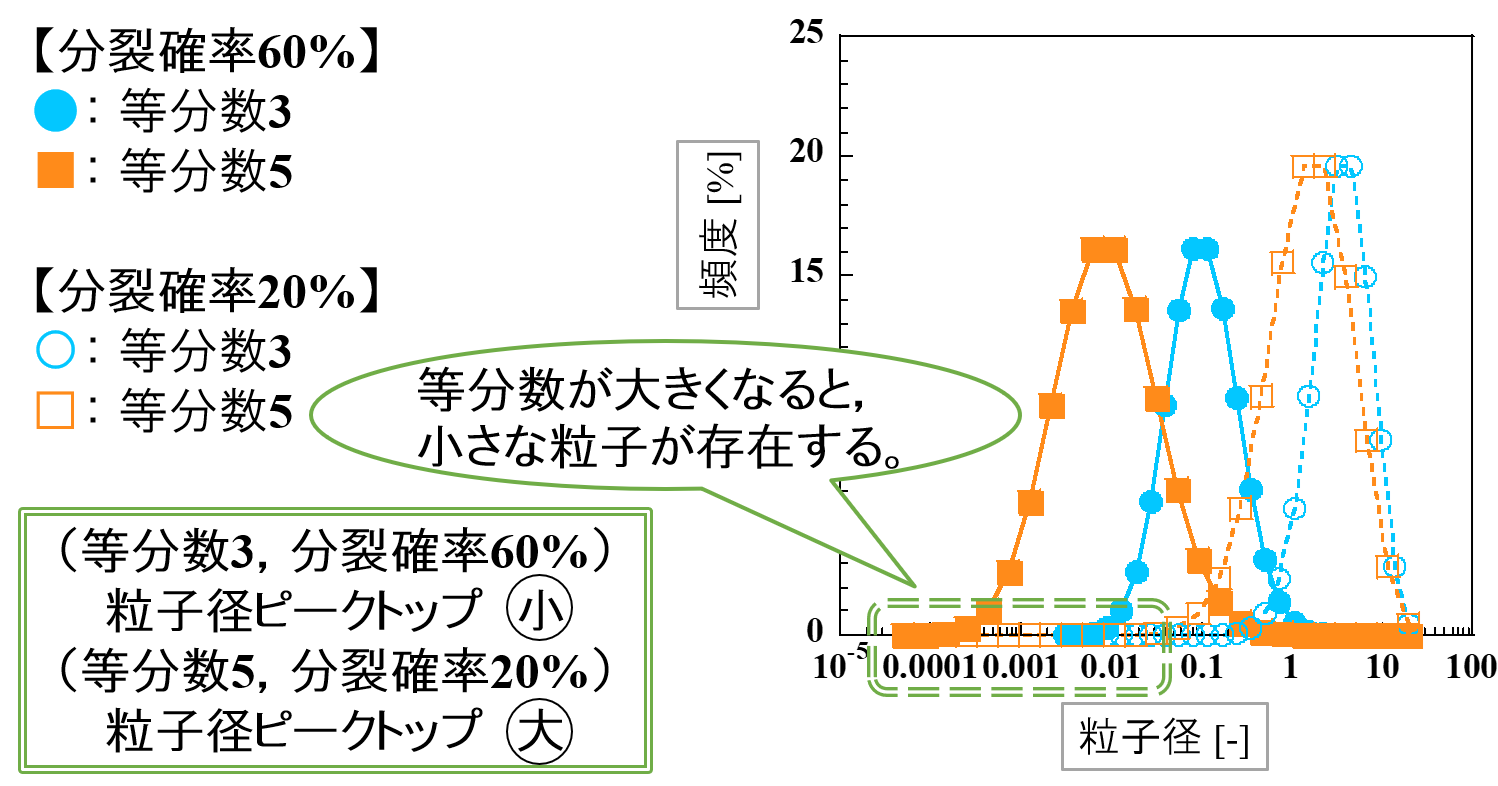
同じことが，各種粒子径にも言えます。

付与するせん断力（等分数）が小さくても，分裂確率が高ければ粒子径（d₅₀, MN, MV）が小さくなることがあり得るということです。

📝[memo]　予期せぬ結果が出たときに，分裂確率が変化した可能性について検討すると良いかもしれません。

同じ撹拌機を使用するのであれば，分裂確率を考えることはなく常に一定であるとみなしています。

そのため，一般的な微細化作用を考える際は，これまで述べてきた粒子径の解釈で良いと思われます。

分裂確率まで変化した！ということまで考慮すると，このように矛盾したように感じる現象が引き起こされる可能性があります。

このような考え方は応用問題になるので，解釈に困ったことがあればヒントにする程度の取り扱いにしておきましょう。

粒子の凝集・破壊モデル

ややこしい話が続いていますが，最後にせん断力と凝集体の関係についての概要を説明して終わりたいと思います。

せん断力場における凝集体について考えた式があるのですが，まずは凝集体の生成速度を示すような式があるとして受け入れることにしましょう。

そして，式を構成する各項が何を示すかを考えてみます。

📝[memo]　多くの文字が登場しますが，”せん断速度ṙ”だけに注目しましょう。

ブラウン凝集： (4α_bk_bTN₀/3η₀)

液中の粒子はブラウン運動によって相対的に粒子間距離が変化し，別の粒子と衝突することを示しています。

式の形は異なりますが，「スケールアップでエマルションを評価しよう【エマルションの安定性（クリーミング）】」のページで紹介したStokesの式と同じことを意味しています。

せん断速度ṙとは無関係の因子であり，粒子同士の衝突という意味では撹拌に直接的な影響を受けないと考えます。

せん断凝集： (4α_sΦnṙ/π), ṙ： 1次

せん断流れ場中に粒子が存在する場合，速度勾配によって粒子間に速度差が生まれ粒子が衝突します。

高速撹拌機による吐出作用の影響と言えるかもしれません。

このとき，せん断速度ṙの影響を受けます。（1次）

せん断破壊： [(3πd₀³n/4F₀N_b){n/(1 – ε) – 1}ηṙ²] , ṙ： 2次

せん断速度が大きい場合には，凝集体が破壊されます。

微細化作用によって生じ得る現象です。

このとき，せん断速度ṙの影響を受けます。（2次）

…というように，なぜこのような話を続けてきたかというと，せん断速度が低い＝せん断力（等分数）が小さいときに凝集が引き起こされることがあることが言いたかったのです。

本来であれば，せん断速度が低くても粒子径が少しだけ小さくなることが想像できますが，逆に大きくなることがあるということです。

• せん断速度が低いとき　…　せん断凝集がせん断破壊を上回る可能性があります。
• せん断速度が高いとき　…　せん断破壊はせん断速度の2次関数として変化するので，1次間数のせん断凝集よりも支配的になります。

---

ちょっとだけ追加でお話をします。

固体に対して過剰な衝撃力やせん断力を与えると，分散した粒子が再凝集することがあります。

過分散と呼ばれており，物性が変化する事例の一つです。

例外的に，せん断力が強ければ小さな粒子が生成しないこともあるということですね。

📝[memo]　おそらく，固体で見られる（＝液体では見られない？）現象ではないかと推察しています。

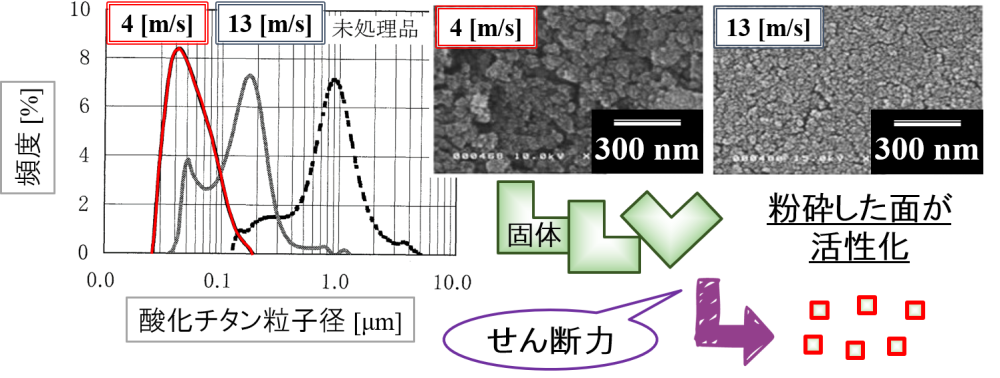
🚩 [引用：針谷 香，橋本和明 J.Jpn.Soc.Colour Mater.，79，136(2006)]

---

エマルションの粒子径について深堀してきましたが，抽象的でややこしくなってきたのでこの辺にしておきます。

分裂確率についても，撹拌機（＋タンク構造）を変更しない限り大きく変化することはないので，あまり深く考えないでおきましょう。

📝[memo]　スケールアップ時においては，原則は同じ撹拌機を使用しますよね。

次回からは，ホモミキサーを機械的な力として考えることにシフトしていきたいと思います。