無次元混合時間

昔，撹拌羽根を使用して次のような実験をした人がいました。

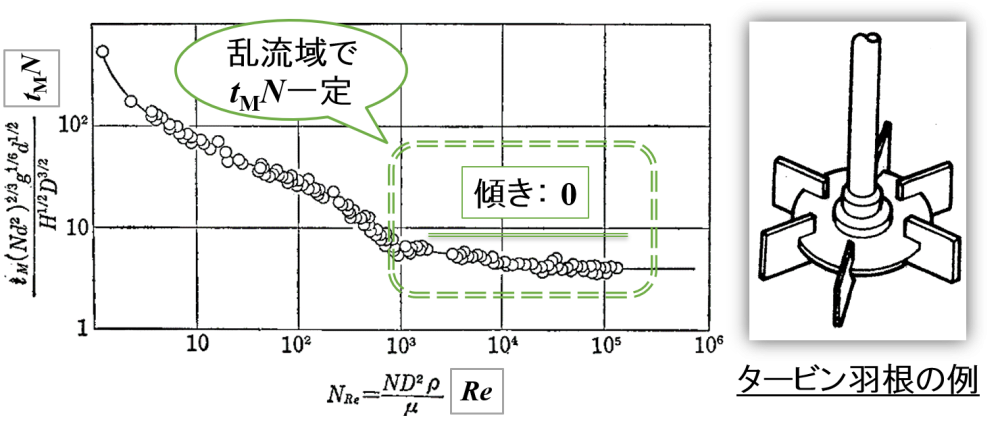
ある撹拌羽根（ここではタービン羽根とします）を用いて，撹拌レイノルズ数Reと混合時間t_Mと回転数Nの積の関係を調べたところ，下図のような傾向があることがわかりました。

「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで紹介したように，通常想定される撹拌機の使用方法であれば，自然と乱流が生じるような撹拌になっていると考えられます。

そこで乱流域に着目すると，グラフの傾きは0とみなすことができます。

すなわち，乱流域では混合時間t_Mと回転数Nの積が一定になります。

🚩 [引用：Norwood, K. W. & Metzner, A. B. A. I. Ch. E. J., 6, 432 (1960)]

混合時間t_Mと回転数Nの積を無次元混合時間t_MNと定義すると，次式のように表現することができます。

無次元混合時間の式を見ると，この値が小さいほうが撹拌能力が高いことがわかります。

📝[memo]　無次元混合時間の値が小さいとき，混合時間は短く，回転数は低くても良いことになります。

最後に，文献値を確認しておこうと思います。

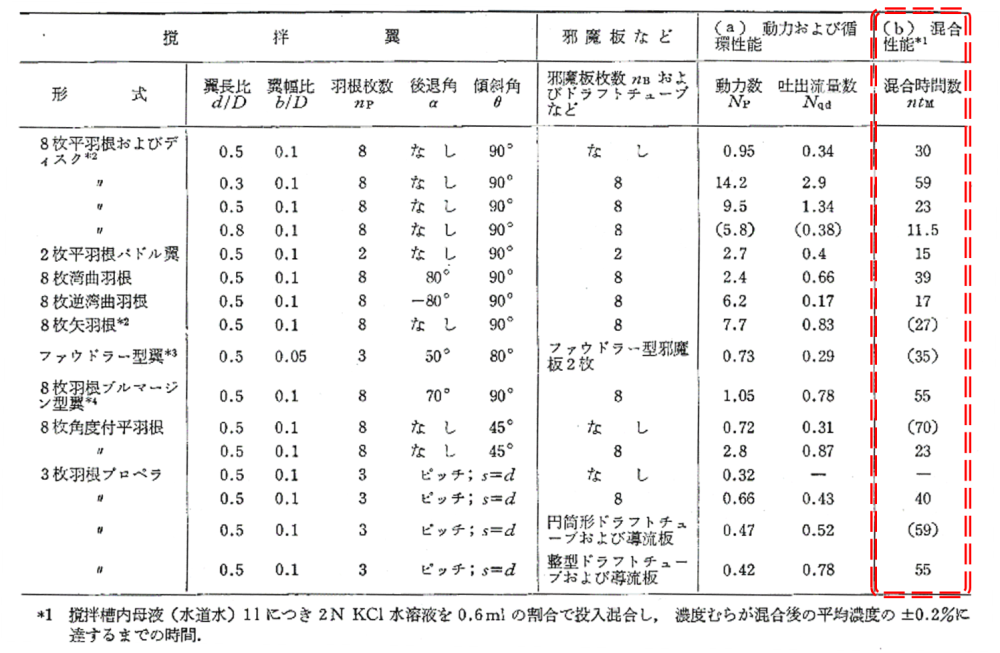
下表は，塩化カリウム水溶液を調製するときの事例です。

表でいうところの「混合時間数」は，上述した「無次元混合時間」と同義です。

様々な撹拌羽根に対して無次元混合時間が記載されており，この値を参考に適切な撹拌羽根を選定することができます。

「混合時間数」＝「無次元混合時間」が小さくなる撹拌羽根が，その混合性能が優れていることを意味します。

🚩 [引用：社団法人化学工学協会編『化学工学便覧』丸善，1988]

液滴が等分される分裂回数と粒子径

低速撹拌機では，無次元混合時間の考え方が採用されていることを確認しました。

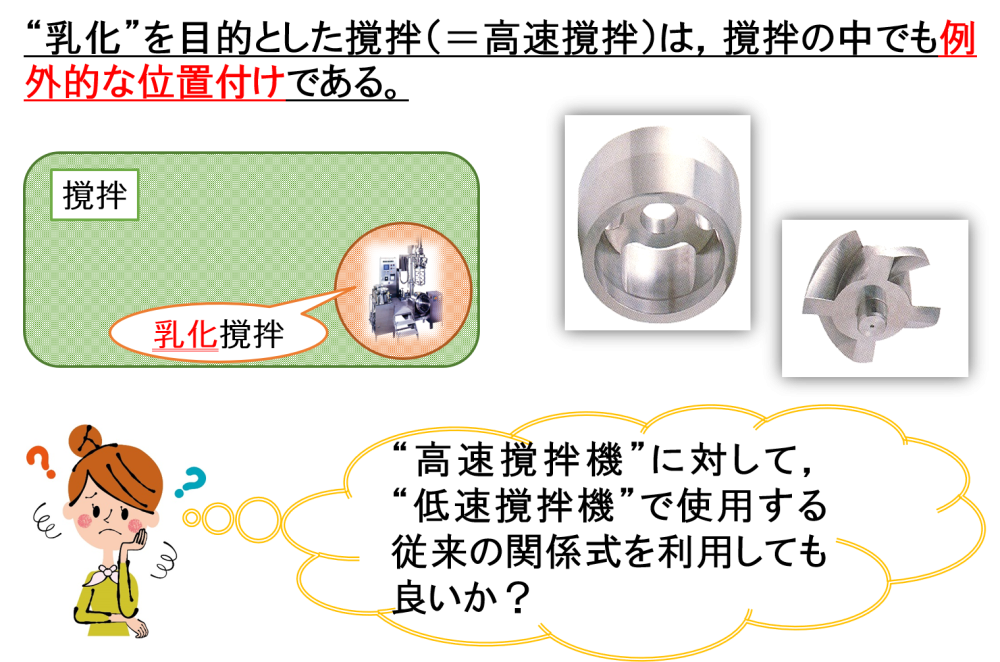
一方，高速撹拌機が例外的な位置づけであるため，低速撹拌機の考え方をそのまま採用しても良いか？という論点があります。

高速撹拌機は，主に微細化作用を発揮することが知られています。

そこで，高速撹拌機によって液滴が分裂していくモデルを考え，この論点について考えていくことにします。

📝[memo]　特に断りがない限り，高速撹拌機はホモミキサーであるとして取り扱います。

📝[memo]　理論化するために計算をしていますが，難しいなと思われた方は読み飛ばしていただいても問題ありません。

液滴の分裂モデル

ここでは，粒子が次々に分裂していく様子をモデル化します。

分裂前（初期状態）

液滴の粒子径（半径）はd₀であるとします。

このときの液滴の体積をV₀とすると，V₀ = (3/4)πd₀³となります。

液滴が1回分裂

1回分裂後の液滴の粒子径（半径）はd₁であるとします。

このときの液滴の体積をV₁とすると，V₁ = (3/4)πd₁³となります。

また，粒子が1回分裂するときn_k等分されたとします。

このときの液滴の体積をV₁とすると，V₁ = (1/n_k)¹V₀ = (1/n_k)¹(3/4)πd₀³となります。

📝[memo]　液滴の総体積は必ず一定になります。V₁ = (1/n_k)¹V₀

📝[memo]　(1/n_k)¹は，あえて1乗を残して表現しています。

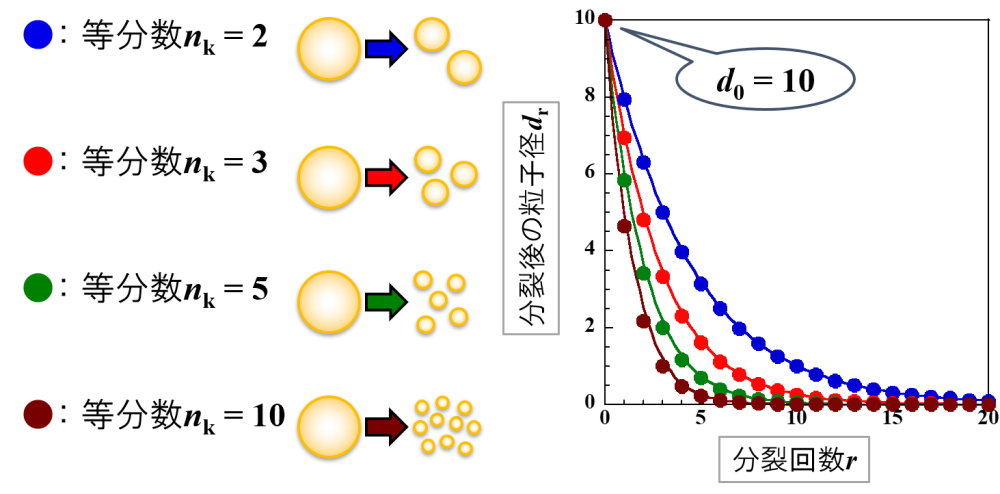
液滴がr回分裂

r回分裂後の液滴の粒子径（半径）はd_rであるとします。

このときの液滴の体積をV_rとすると，V_r = (3/4)πd_r³となります。

また，粒子が1回分裂するときn_k等分されたとします。

📝[memo]　粒子が1回分裂するときの等分数n_kは，常に一定で変化しないと仮定します。

このときの液滴の体積をVrとすると，V_r = (1/n_k)^rV₀ = (1/n_k)^r(3/4)πd₀³となります。

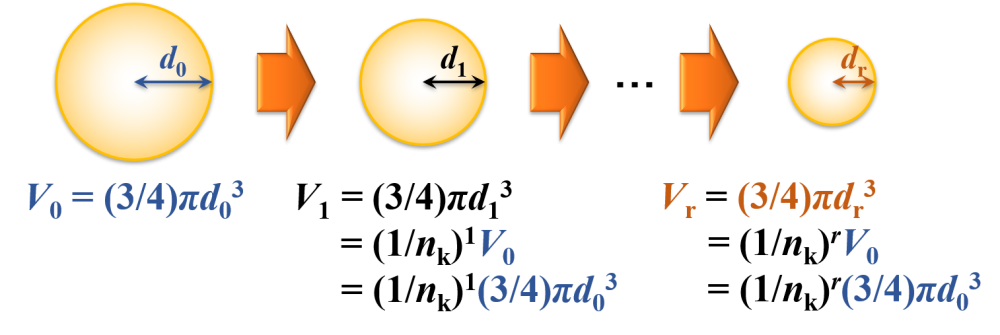
分裂後の粒子径を決める因子

このようなモデルは，次式のように表現することができます。

式の形を見る限り，無次元混合時間の考え方とは異なっていることがわかります。

「撹拌をやさしく捉えてみよう【撹拌の考え方】」のページで紹介したように，液滴を微細化するためには撹拌による微細化作用が必要でした。

液滴に対して大きな微細化作用を付与すると，小さな液滴が得られると考えられます。

より小さな液滴が生成するためには，できるだけ複数に分裂する必要があります。

📝[memo]　体積を一定に保ちながら小さな液滴になるためには，その個数は多くなります。

分裂して生じる液滴の数は，等分数n_kによって決まります。

したがって，液滴に対して大きな微細化作用を付与すると，等分数n_kが大きくなると考えることができます。

ただし，これ以上小さくならないような微小な液滴が生成したときは，等分数n_kが0に近づいていきます。

微細化作用の大きさによって，最大の等分数n_kが決定されると言った方が良いかもしれません。

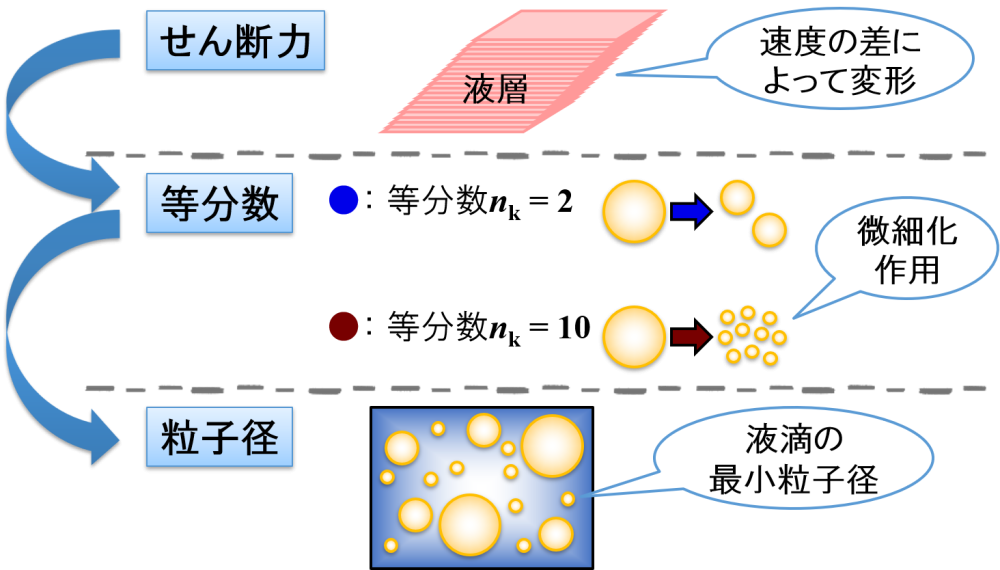
さらに，「撹拌をやさしく捉えてみよう【撹拌をどのように利用するべきか？】」のページで紹介したように，微細化作用を引き起こすための具体的な力はせん断力がメインでした。

そこで，”微細化作用”を”せん断力”に置き換えると…，

液滴に対して大きなせん断力を付与すると，等分数n_kが大きくなると考えることができます。

一方，「撹拌をやさしく捉えてみよう【低速撹拌機と高速撹拌機】」のページで紹介したように，ホモミキサー（タービン羽根）を通過することで微細化作用が働きます。

このとき，タービン羽根を通過する回数が多いほど，液滴はより小さくなっていきます。

すなわち，分裂回数rはタービン羽根を通過する回数に依存すると考えることができます。

回転数とパス回数

等分数n_kや分裂回数rは，独自の表現であり聞きなじみがありません。

そこで，高速撹拌機による条件は一般的に「回転数」と「乳化時間」で表すことが多いため，これらに置き換えることが理想的です。

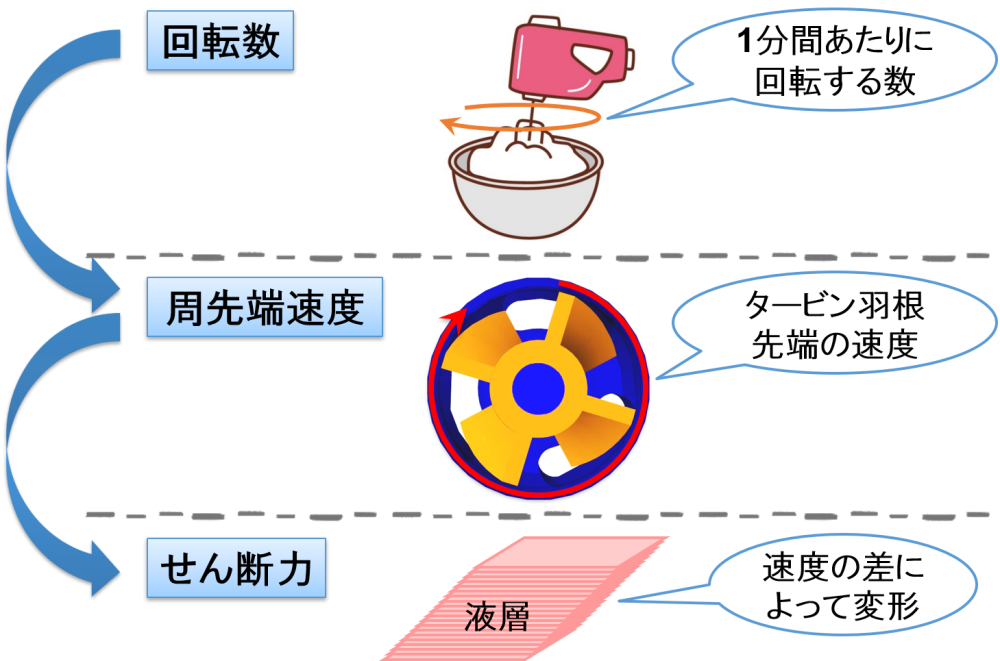
回転数

回転数とは，”1分間あたりに回転する数”を意味します。

これは，”1分間あたりにタービン羽根先端が進む速度（＝周先端速度）”と言い換えることができます。

一方で，液滴に対して大きなせん断力を付与すると，等分数n_kが大きくなると考えました。

速度の差によって変形が生じる力を”せん断力”と呼んでいるので，せん断力は回転数に依存すると考えられます。

そして，液滴に対して大きな微細化作用を付与すると等分数n_kが大きくなると考えたので，微細化作用＝せん断力となります。

すなわち，回転数を高くすることによって等分数n_kが大きくなり，より小さな液滴を生成できるようになります。

📝[memo]　「スケールアップ理論を考えてみようー乳化編【高速撹拌機による液滴の微細化】」のページで，どこまで液滴を小さくすることができるかについて議論することにします。

📝[memo]　撹拌機の回転数を高くすることによってより小さな液滴を生成できるようになる（＝等分数n_kが大きくなる）ため，必要な分裂回数rを減らす（＝乳化時間を短くする）ことができます。

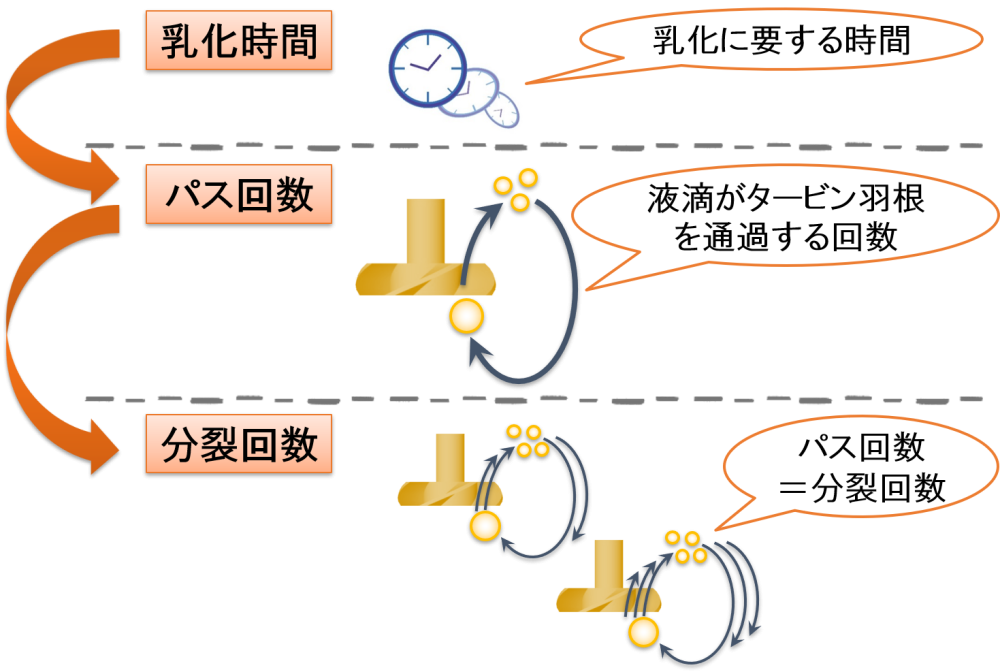
乳化時間

乳化時間とは，言葉通り”乳化に要する時間”です。

したがって，液滴がタービン羽根を通過する回数（＝パス回数）と置き換えることができます。

📝[memo]　乳化時間が長いことは，パス回数が多いことを意味します。

分裂回数rはタービン羽根を通過する回数として考えたので，パス回数＝分裂回数rです。

したがって，分裂回数rは乳化時間に依存すると考えられます。

分裂回数rが増えると，液滴が微細化される機会が増えます。

あらゆる大きさの液滴がタービン羽根を通過するので，液滴の粒度分布が均一になっていきます。

すなわち，乳化時間を長くすることによって分裂回数rが多くなり，より均一な液滴を生成できるようになります。

---

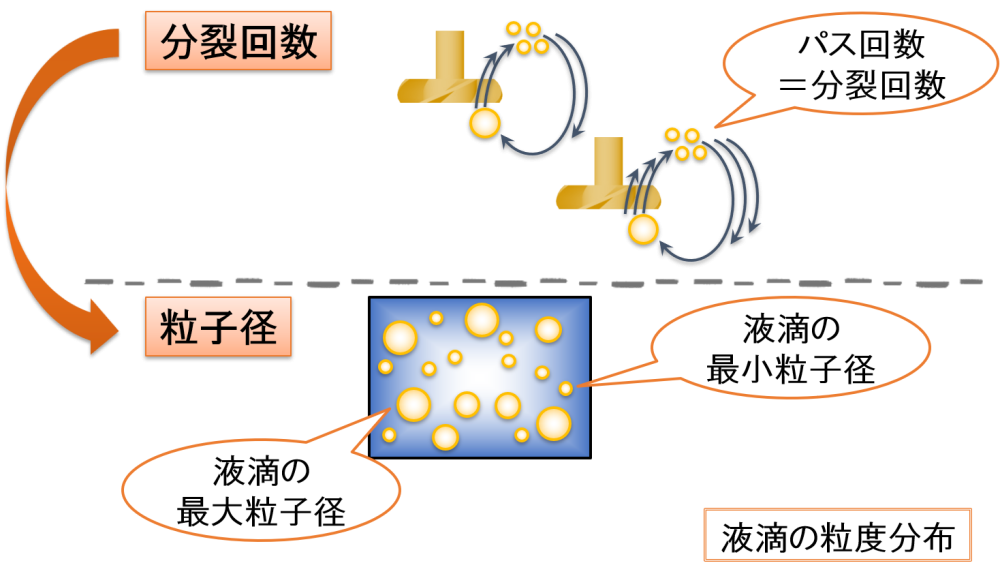
一方で，パス回数を増やすためには，液滴が速く動いてくれれば良いと考えることもできます。

液滴が速く動くと，液滴がタービン羽根を通過する回数が増えます。

すなわち，吐出量を増やすことを意味します。

📝[memo]　「スケールアップ理論を考えてみよう ー 乳化編【“ホモミキサー”による吐出量】」のページで吐出量の式を紹介しており，吐出量は回転数に比例します。

したがって，回転数を高くすることによっても，パス回数を多くすることができます。