機械的な力によって液滴が分裂する条件

少しだけ，理論的な話が続きます。

「スケールアップ理論を考えてみようー乳化編【回転数・混合時間/乳化時間の考え方】」のページで，液滴に対して大きなせん断力を付与すると等分数n_kが大きくなり，分裂し続けるような説明をしました。

しかしながら，このような考え方は実態とは異なっており，分裂を起こす最小せん断応力が存在します。

📝[memo]　不正確な点を含むイメージとなりますが，ここでは「液滴に付与する力＝せん断力」，「液滴が付与される力＝せん断応力」としてください。

臨界ウェーバー数

新たな考え方は，”臨界ウェーバー数”として知られています。

注目すべき点は，やはり分裂を起こす最小せん断応力τ_Bです。

ここで，臨界ウェーバー数(We)_cと界面張力γは物性値であるため定数です。
液滴に対して大きな微細化作用を付与すると液滴は複数個に分裂するので，分裂で生成する粒子径dは変数と言えます。

液滴の粒子径dが小さくなると，分裂を起こす最小せん断応力τ_Bが大きくなることがわかります。

撹拌によるせん断力を液滴に付与した結果，分裂を起こす最小せん断応力τ_Bを超えることができれば液滴は複数個に分裂します。

ただし，撹拌によるせん断力は限界値があるため，微細化できる最終的な液滴の粒子径が決まってきます。

等分数と液滴が受けるせん断応力の関係

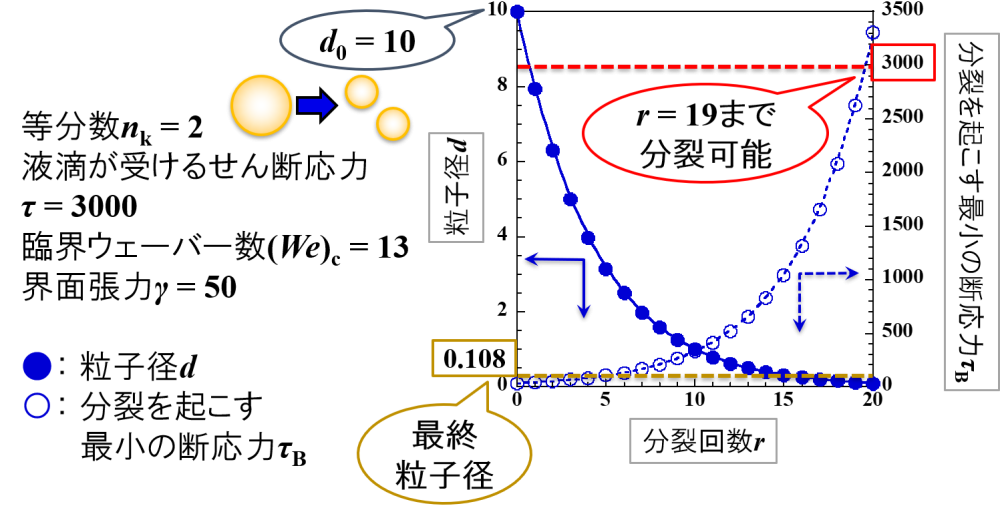
例えば，「等分数n_k = 2，液滴が受けるせん断応力τ = 3000，臨界ウェーバー数(We)_c = 13，界面張力γ = 50」の場合を考えます。

液滴が2つに分裂（等分数n_k = 2）し，分裂回数を重ねるごとに粒子径dが小さくなっていきます。（下図●）

一方，液滴の分裂回数を重ねるごとに粒子径dが小さくなるため，分裂を起こす最小せん断応力τ_Bが大きくなっていきます。（下図〇）

このとき，分裂20回目で分裂を起こす最小せん断応力τ_Bが3000を超えます。

撹拌によって液滴が受けるせん断応力は3000なので，分裂は19回目までしか起こりません。

最終粒子径dは0.108となり，液滴はこれ以上小さくなりません。

液滴を小さくする手法

液滴を小さくするためには，分裂を起こす最小せん断応力τ_Bを超えるせん断力を液滴に付与しなければなりません。

そのためには，主に2つの手法が考えられます。

界面張力γを小さくする

界面張力γを小さくすると，分裂を起こす最小せん断応力τ_Bも小さくなります。

その結果，液滴を小さくすることができます。

「撹拌の立場から乳化をイメージしよう【ギブス自由エネルギーと乳化現象②】」のページで紹介したように，界面張力γを小さくするために界面活性剤を添加していましたよね。

どちらかと言うと，「処方的な力」の役割となります。

せん断力を大きくする

そもそも付与するせん断力自体を大きくすれば分裂を起こす最小せん断応力τ_Bを超えることができるので，液滴を小さくすることができます。

このとき，「撹拌をやさしく捉えてみよう【低速撹拌機と高速撹拌機】」のページで紹介したような微細化作用を発揮する高速撹拌機を使用します。

📝[memo]　撹拌機以外の装置を使用することもあります。ex. 高圧乳化装置

どちらかと言うと，「機械的な力」の役割となります。

これまでにも同じような話をしてきましたが，”臨界ウェーバー数”という別の考え方から同様のアプローチをすることができました。

“高速撹拌機”による理論上の粒子径の変化

以上の理論的な考え方（液滴の分裂モデル・臨界ウェーバー数）を踏まえて，高速撹拌機による回転数や乳化時間を変化させると，液滴の粒子径がどのように変化するかイメージしてみましょう。

液滴の粒子径は，粒度分布の変化から考えることができます。

📝[memo]　すべての製品について当てはまるとは限りませんが，これまでに紹介してきた理論と経験的な話を織り交ぜながら説明します。

粒度分布で考える

ここで，粒度分布を考えること自体について端的に説明しておきます。

📝[memo]　難しいなと思われた方は読み飛ばしていただいても問題ありません。

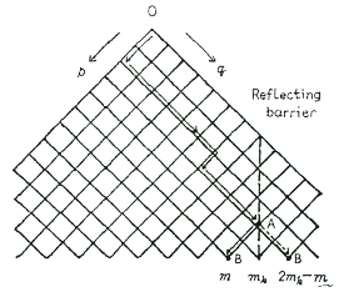
液滴の分裂が起こる確率をp，起こらない確率をqとすると，右図で示すように確率pで左に，確率qで右に行くようなランダムウォークを示すと仮定します。

このとき，Stirlingの式を適用することによって，mの位置に存在する液滴の確率を求めることができます。

そして，結論として液滴の存在確率は正規分布に近似されるので，液滴の粒子径は粒度分布で表現できるとして考えることにします。

📝[memo]　ただし，p = q = 1/2のときに成り立ちます。

ホモミキサーの通過確率 ＝ 50％

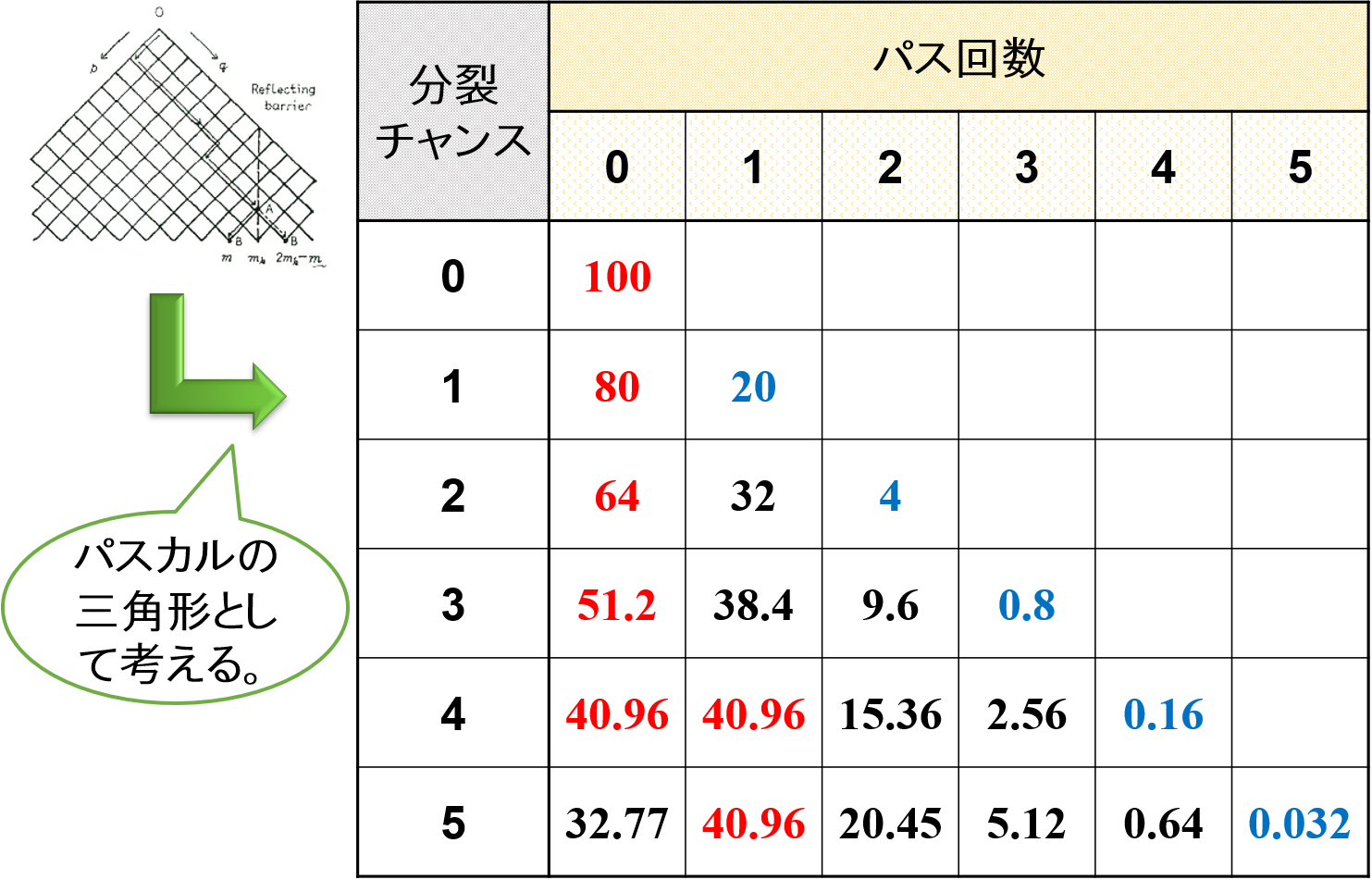
そして，このランダムウォークをパスカルの三角形として考えることをします。

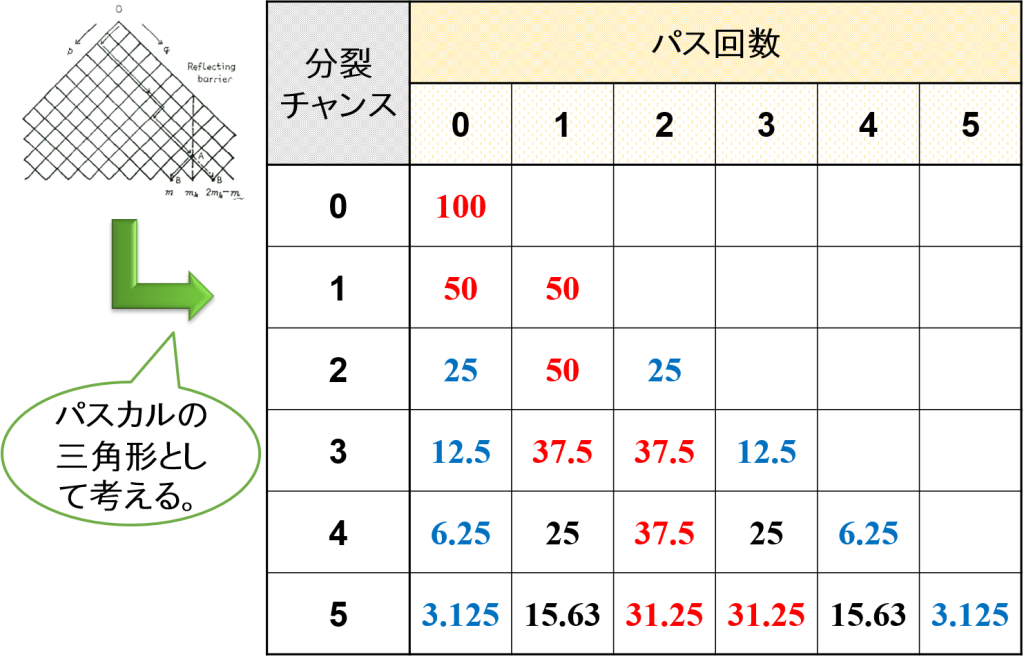
例えば，理論上，液滴がホモミキサーを通過して5回分裂するチャンスがあったと仮定します。

このとき，ホモミキサーを通過（パス）する確率を50%とします。

すると，液滴が5回分裂する確率は(1/2)⁵ = 1/32 = 0.03125であり，約3%であることがわかります。

理想通りに液滴を5回分裂させることは難しく，ほとんど起こりえないと言えます。

一方，液滴が2回分裂する確率は10/32 = 0.3125，液滴が3回分裂する確率も10/32 = 0.3125であり，併せて約62.5%であることがわかります。

これは，液滴が2または3回分裂する確率が一番高いことを意味します。

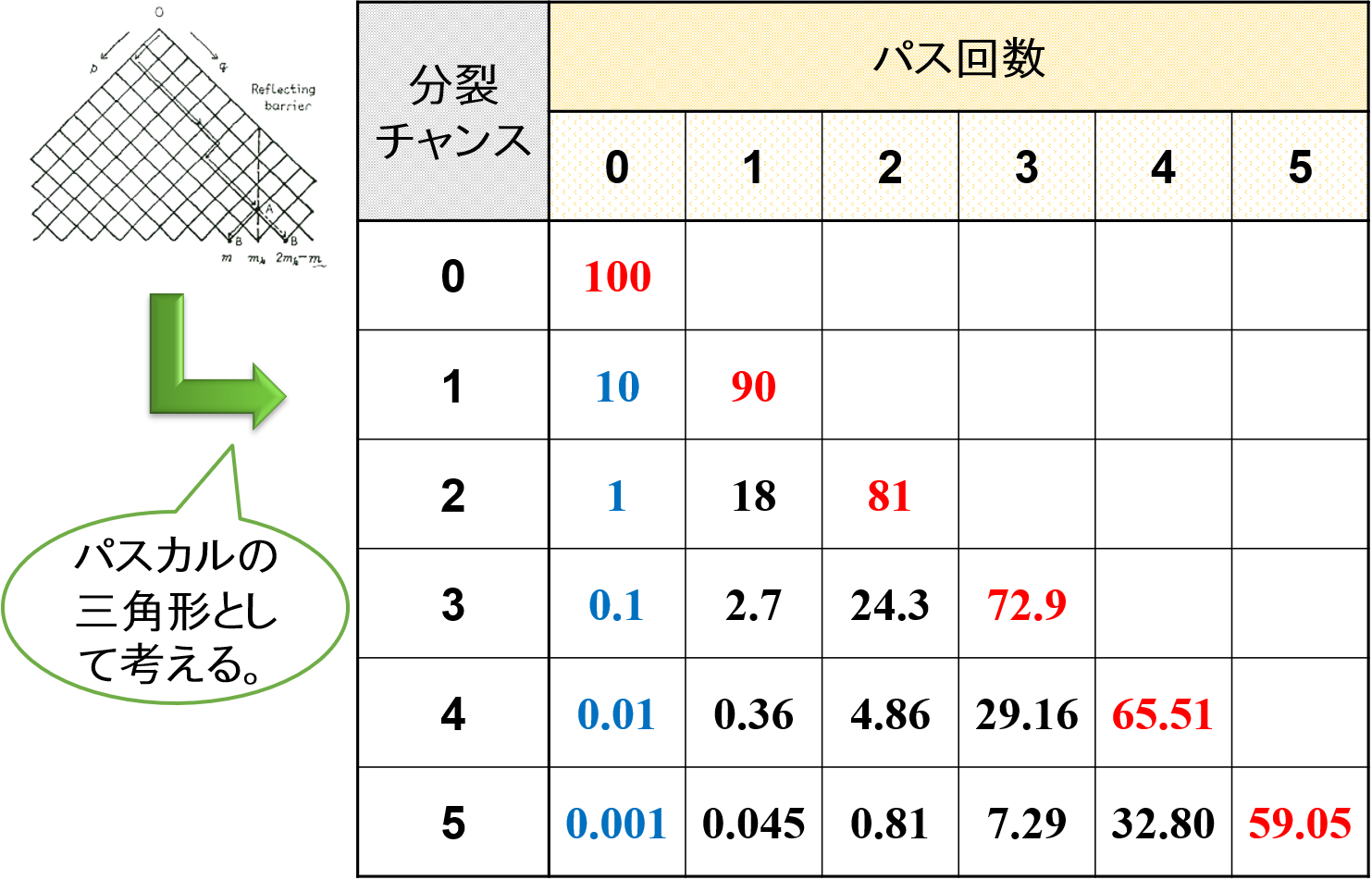
ホモミキサーの通過確率 ＝ 90%

ホモミキサーを通過する確率が90%まで高くなったとき，5回分裂するチャンスがあったと仮定すると液滴が5回分裂する確率が一番高くなっています。

📝[memo]　液滴が5回分裂する確率は(9/10)⁵ = 0.59049（＝約59%）であり，6割近くが理想通りになっています。

4回分裂した液滴を含めると，全体の80%以上を占めていることがわかります。

上述した「ホモミキサーの通過確率 ＝ 50％」のときよりも，撹拌機は良い働きをしています。

ホモミキサーの通過確率 ＝ 20%

一方で，ホモミキサーを通過する確率が20%まで低くなったとき，5回分裂するチャンスがあったと仮定すると液滴が1回分裂する確率が一番高くなっています。

📝[memo]　液滴が5回分裂する確率は(2/10)⁵ = 0.00032（＝約0.032%）であり，全くと言っていいほど理想的な撹拌機の動きはしていません。

0回分裂（＝分裂しない）した液滴を含めると，全体の70%以上を占めていることがわかります。

この結果は，撹拌機としての役割をほとんど果たしていないと評価することができます。

“高速撹拌機”による回転数変化イメージ（“最終粒子径”到達前）

これ以降は，ホモミキサーを通過する確率は一定であると仮定して話を進めていきます。

ここでの事例では，ホモミキサーを通過する確率＝分裂確率＝60%として考えています。

乳化時間は一定で，回転数だけを変化させたとします。

高速撹拌機の回転数を低速から高速へ上げていくことを考えます。

そして，高速撹拌機が高速になり分裂回数が多くなり，分裂を起こす最小せん断応力τ_Bに達したと仮定します。

このとき，エマルションの粒度分布は下図のように変化する傾向があります。

📝[memo]　下図においては，回転数（等分数）： 4で乳化時間（分裂回数）： 18のときに，分裂を起こす最小せん断応力τ_Bに達したと仮定します。

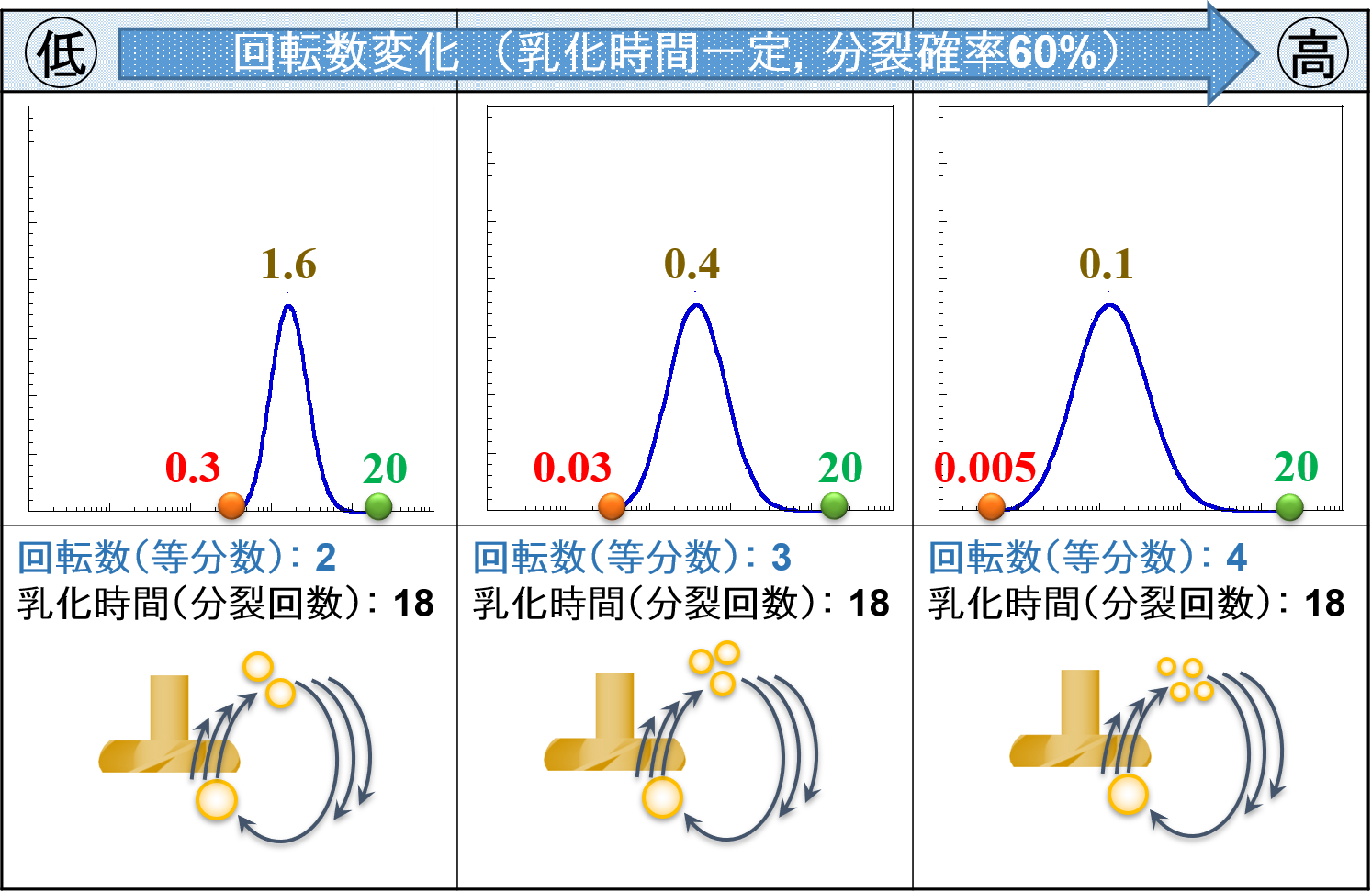
「スケールアップ理論を考えてみようー乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介したように，回転数が高くなると等分数n_kが大きくなります。

したがって，乳化時間一定であれば，回転数が高くなるほど全体の粒子径が小さくなると言えます。

一番小さな粒子径d_minは0.3 → 0.03 → 0.005，一番大きな粒子径d_maxは20から変化していませんがその存在割合は低くなっています。

📝[memo]　理論上，どのような撹拌条件であっても，大きさが20の液滴が低確率で残存してしまします。

分裂を起こす最小せん断応力τ_Bに達するまでは，回転数が高くなると液滴全体の粒子径が小さくなると言えます。

📝[memo]　すべての液滴に対し，ホモミキサーは同じ割合でせん断力を付与していると考えるので，同じような分布を保持したまま液滴が全体的に小さくなっていくと想像できます。

“高速撹拌機”による乳化時間変化イメージ（“最終粒子径”到達前）

回転数は一定で，乳化時間だけを変化させたとします。

📝[memo]　このときの回転数は，分裂を起こす最小せん断応力τ_Bに達していると仮定します。

このとき，エマルションの粒度分布は下図のように変化する傾向があります。

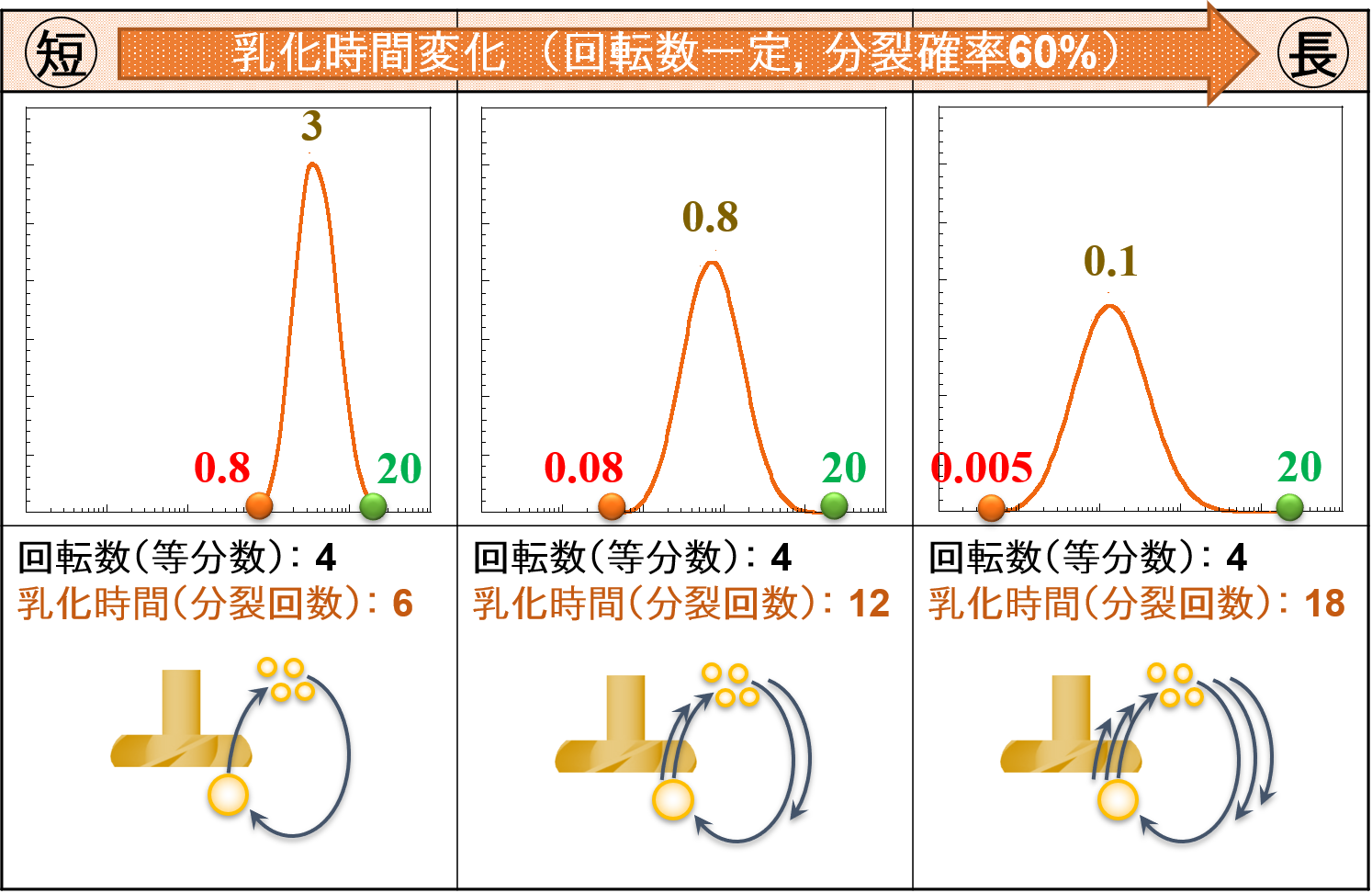
「スケールアップ理論を考えてみようー乳化編【回転数・混合時間/乳化時間の考え方】」のページで紹介したように，回転数が一定であれば等分数n_kは変化しないと考えました。

📝[memo]　“最終粒子径”到達後には，等分数n_kが0に近づいていきます。

しかしながら，乳化時間が長くなると分裂回数が多くなるので，液滴の大きさに関係なく全体の粒子径が小さくなると言えます。

一番小さな粒子径d_minは0.8 → 0.08 → 0.005，一番大きな粒子径d_maxは20から変化していませんがその存在割合は低くなっています。

📝[memo]　乳化時間を長くしてパス回数を多くすると，大きな粒子が小さくなる確率が高くなります。

“最終粒子径”到達後のイメージ

“最終粒子径”到達前において，回転数を高くしたりパス回数を多くすると，その過程は異なりますが液滴全体が小さくなることを考えました。

続いて，分裂を起こす最小せん断応力τ_Bに達した後の変化を考えます。（“最終粒子径”到達後）

高速撹拌機をさらに高速にすると，分裂を起こす最小せん断応力τ_Bよりも大きなせん断力を付与できるようになります。

その結果，液滴はさらに分裂することができるため，下図で示すように一番小さな粒子径d_minが0.005 → 0.001へと変化します。

すなわち，高速撹拌機をさらに高速にすると，小さな液滴がさらに小さくなる傾向が見られます。（同時に大きな液滴も小さくなります）

一方，乳化時間をさらに長くしても，分裂を起こす最小せん断応力τ_Bよりも大きなせん断力を付与することはできません。

そのため，一番小さな粒子径d_minは変化しません。

ただし，大きな液滴はさらに小さくなることができるのでその存在割合は低くなり，一番小さな粒子径d_minへと近づいていきます。

すなわち，乳化時間をさらに長くすると大きな液滴のみが小さくなり，液滴の粒度分布が均一になる傾向が見られます。

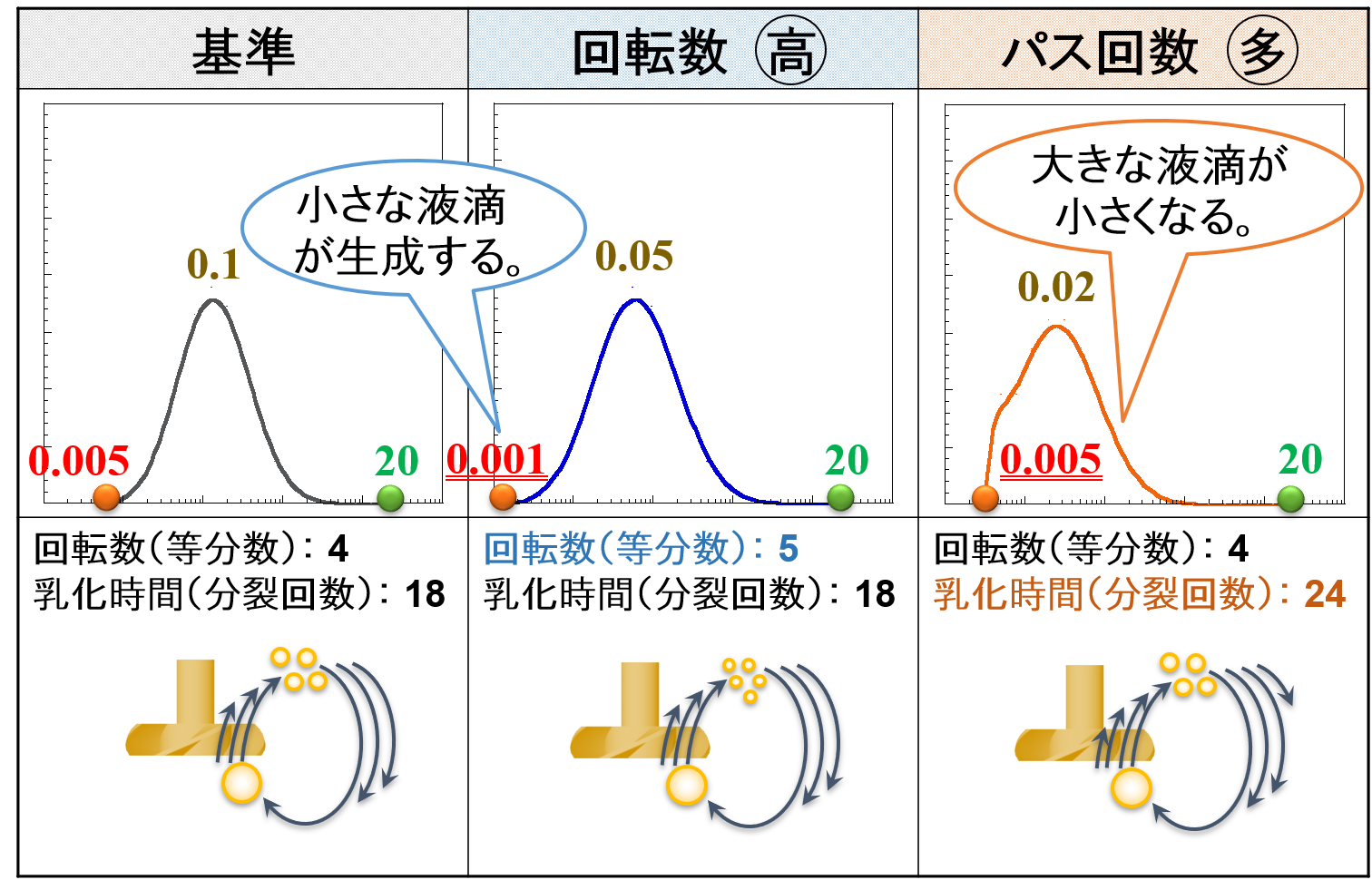
“最終粒子径”到達前は，液滴が小さくなるメカニズム（等分数と分裂回数）は異なりましたが，回転数を高くした場合や乳化時間を長くした場合は，いずれも液滴が小さくなる傾向がありました。

“最終粒子径”到達後は，回転数と乳化時間によって撹拌機の働きが異なることがわかります。