撹拌作用を使い分ける

「撹拌をやさしく捉えてみよう【撹拌をどのように利用するべきか？】」のページで，使用する”撹拌作用”によって最終状態が異なることを紹介しました。

例えば，1つの容器の中に「液体A」と「固体B」が入っているとき，「固体B」を動かす必要がある工程では，撹拌による”吐出作用”を発揮すると良いことが直感的にわかります。

一方で，「固体B」を細かくする必要がある工程では，撹拌による”微細化作用”を発揮すると良いことが直感的にわかります。

しかしながら，撹拌を使用する工程は，このようなわかりやすい事例ばかりとは限りません。

それでは，これらの”撹拌作用”をどのように使い分けたら良いでしょうか？

”吐出作用”を利用すべき例

最初に，「吐出作用を利用すべき例」について考えてみたいと思います。

”吐出作用”を利用すべき例として，例えば，食塩の溶解が挙げられます。

「撹拌の立場から乳化をイメージしよう【ギブス自由エネルギーと乳化現象①】」のページで説明しましたが，水の中に食塩を入れるだけで食塩水が完成します。

すなわち，どれだけ時間がかかるかはわかりませんが，放置したままにしておいても最終的に食塩水ができあがります。

下図で紹介している事例は，どれだけ時間がかかるかはわかりませんが，放置したままにしておいても最終的な状態ができあがるものを示しています。

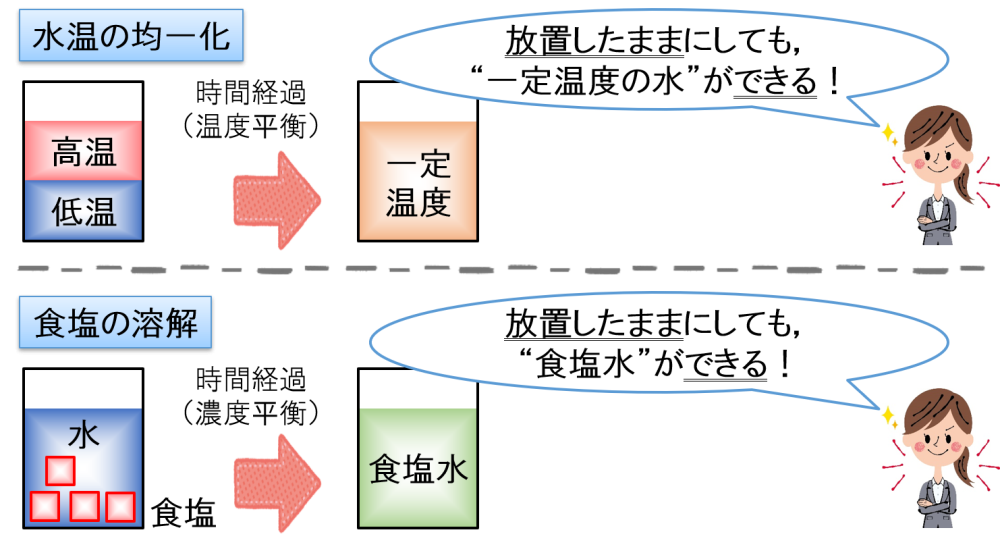
…ということで，「吐出作用を利用すべき例」についてまとめると…，

時間経過で自然に引き起こされる現象に対しては，通常，撹拌による大きな”吐出作用”を利用すると良い場合が多いと言えます。

”微細化作用”を利用すべき例

次に，「微細化作用を利用すべき例」について考えてみたいと思います。

”微細化作用”を利用すべき例として，例えば，エマルションの調製が挙げられます。

「撹拌の立場から乳化をイメージしよう【ギブス自由エネルギーと乳化現象②】」のページで説明しましたが，エマルションを調製するためには，油相・水相・界面活性剤が必要です。

そして，「撹拌の立場から乳化をイメージしよう【エマルションの調製と機械的な力】」のページで説明しましたが，乳化するためには撹拌によって油滴を生成しなければなりません。

したがって，放置したままにしておいても最終的にエマルションはできあがりません。

粉体の分散（微細化）も同様です。

2種類の固体を入れた容器を放置したままにしておいても，それぞれの固体が細かくなって混ざってくれません。

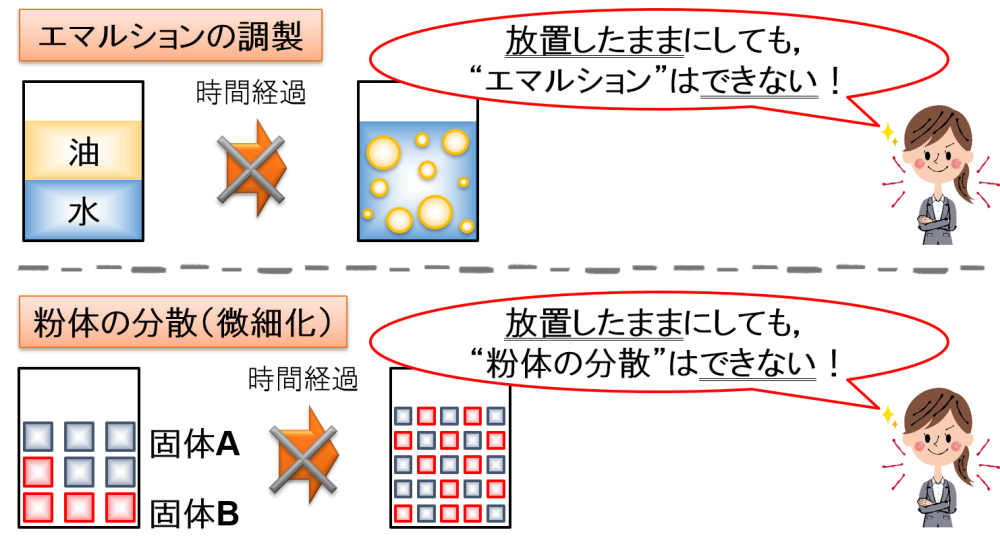
…ということで，「微細化作用を利用すべき例」についてまとめると…，

時間経過で自然に引き起こされない現象に対しては，通常，撹拌による大きな”微細化作用”を利用すると良い場合が多いと言えます。

“吐出作用”+“微細化作用”を利用すべき例

最後に，「吐出作用と微細化作用を利用すべき例」について考えてみたいと思います。

”吐出作用”と”微細化作用”を利用すべき例として，例えば，増粘剤の分散が挙げられます。

どれだけ時間がかかるかはかりませんが，放置したままにしておいても増粘剤の水分散液ができあがります。

しかしながら，微細化作用によって増粘剤を細かくした方が，その表面積が大きくなるので水中に拡散しやすくなります。

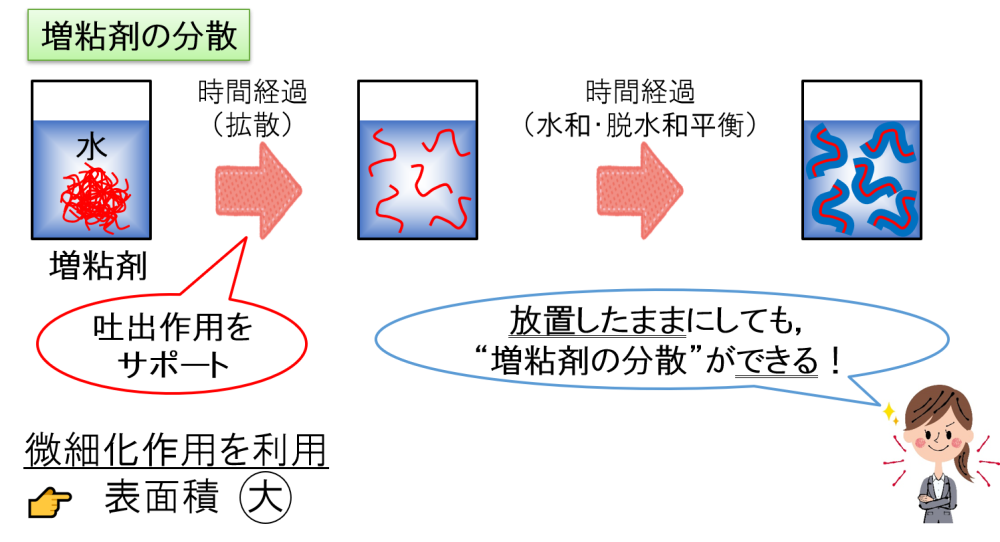
本来であれば，撹拌による大きな”吐出作用”を利用すると良いと考えることができます。

ただ，微細化作用を併用することで，吐出作用をサポートする働きをすることができます。

一方で，固体の溶解に関するNernst-Brunner/Noyes-Whitneyの式からも，数学的に次のように理解することができます。

📝[memo]　難しい話なので，このような式が知られていることを前提とします。

• 分散質の表面積A 大　（＝粒子径d 小）　👉　溶解速度dX/dt 大
• 分散質の表面積A 小　（＝粒子径d 大）　👉　溶解速度dX/dt 小

物質の粒子径が小さくなるに従い流体（水）と接触する表面積Aが増大するので，流体（水）への溶解速度dX/dtが大きくなることがかります。

“吐出作用”と“微細化作用”のイメージ

吐出作用は物質を動かすことができ，微細化作用は物質を細かくすることができます。

これらの”撹拌作用”の働きを拡張して，どのように使い分けたら良いかを考えました。

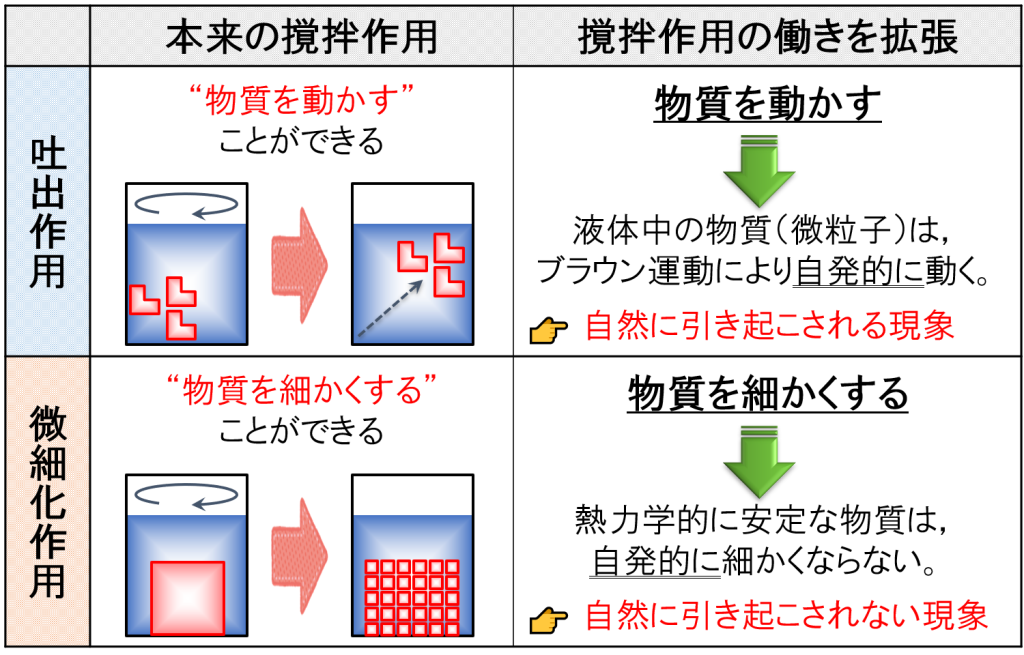
次に，このような使い分けをどのようにイメージしたら良いかを考えることにします。

吐出作用のイメージ

自然に引き起こされる現象に対しては，”吐出作用”を使う撹拌をすれば良いことがわかりました。

「自然に引き起こされる」ということは，ボールが坂道を転がっていくような現象に例えることができます。

どれだけ時間がかかるかはわかりませんが，放置したままにしておいても最終的にボールは転がっていきますよね。

したがって，”吐出作用”を使うことによって，ボールが坂道を速く転がるような作用を与えているようなイメージになります。

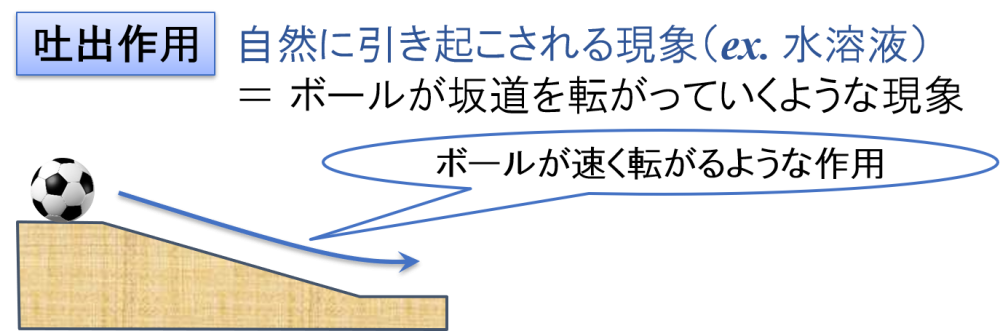
これは，「時間短縮」して，必要生成物を迅速に生産することを可能にする働きを持っていることを意味します。

微細化作用のイメージ

自然に引き起こされない現象に対しては，”微細化作用”を使う撹拌をすれば良いことがわかりました。

「自然に引き起こされない」ということは，ボールが坂道を上っていくような現象に例えることができます。

放置したままにしておいても，ボールはその場に留まっているだけで坂道を上っていくことはありませんよね。

したがって，”微細化作用”を使うことによって，ボールを強制的に持ち上げるような作用を与えているようなイメージになります。

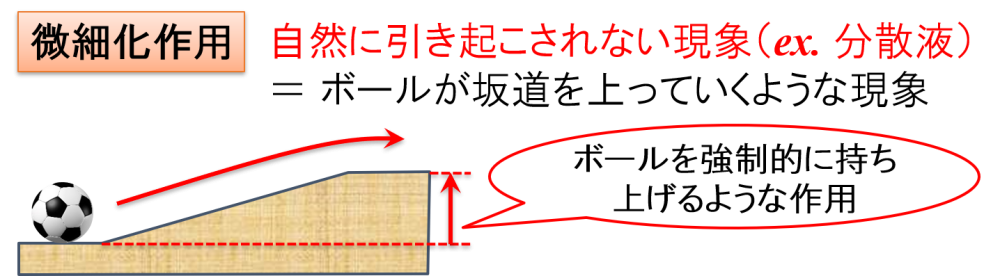
これは，自然現象では起こり得ない「新物質」（＝「新状態」）を作り出すことを可能にする働きを持っていることを意味します。

撹拌エネルギー

“吐出作用”と“微細化作用”について紹介してきましたが，これらを発揮するためには動力源となる”撹拌エネルギー”が必要になります。

撹拌エネルギーを表す式は複雑な形をしていますが，ポイントになるのは，「撹拌エネルギーPは微細化作用Heと吐出作用Qの積に比例する」ということです。

数学的にいえば，「微細化作用Heと吐出作用Qは反比例の関係にある」ということですが，これはどういったことを意味するのでしょうか？

そこで，縦軸を微細化作用He，横軸を吐出作用Qをとしたグラフ（図形）を考えてみたいと思います。

このとき，撹拌エネルギーPは微細化作用Heと吐出作用Qの積に比例するので，四角形の面積の大きさとして表されることになります。

📝[memo]　四角形の面積P＝縦軸He×横軸Q

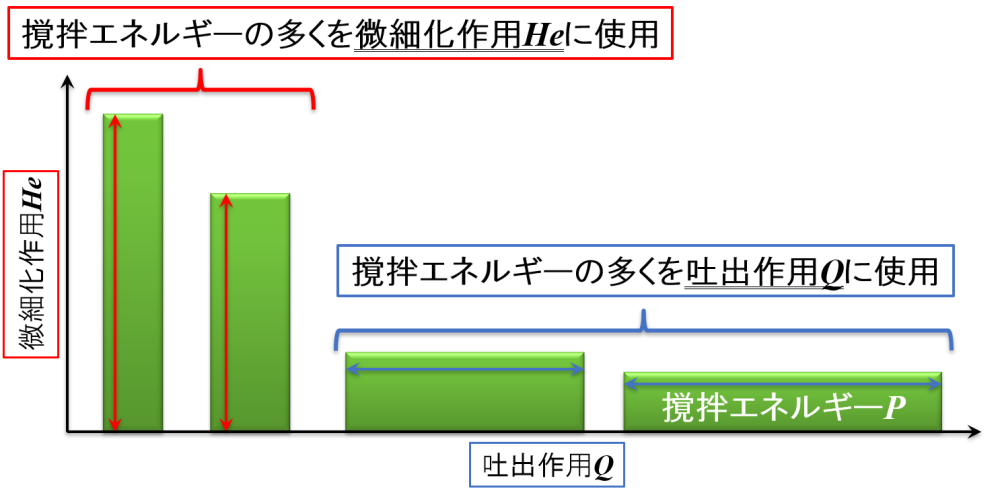
例えば撹拌エネルギーPが一定であったとして，さらに次のような場合を考えてみます。

微細化作用Heが大きいとき

撹拌エネルギーPの多くを微細化作用Heに使用すると，撹拌エネルギーPは縦軸（微細化作用He）が長い四角形として表されます。

その結果，横軸が短くなるので吐出作用Qが小さくなることがわかります。

📝[memo]　右図の四角形のような場合です。

吐出作用Qが大きいとき

撹拌エネルギーPの多くを吐出作用Qに使用すると，撹拌エネルギーPは横軸（吐出作用Q）が長い四角形として表されます。

その結果，縦軸が短くなるので微細化作用Heが小さくなることがわかります。

📝[memo]　下図の四角形のような場合です。

---

このように考えると，撹拌エネルギーが同じであっても撹拌機としての能力が異なってくることが理解できるかと思います。

• 撹拌エネルギーPの多くを微細化作用Heに使用する（微細化作用Heが大きくなる）と，吐出作用Qが小さくなります。
• 撹拌エネルギーPの多くを吐出作用Qに使用する（吐出作用Qが大きくなる）と，微細化作用Heが小さくなります。

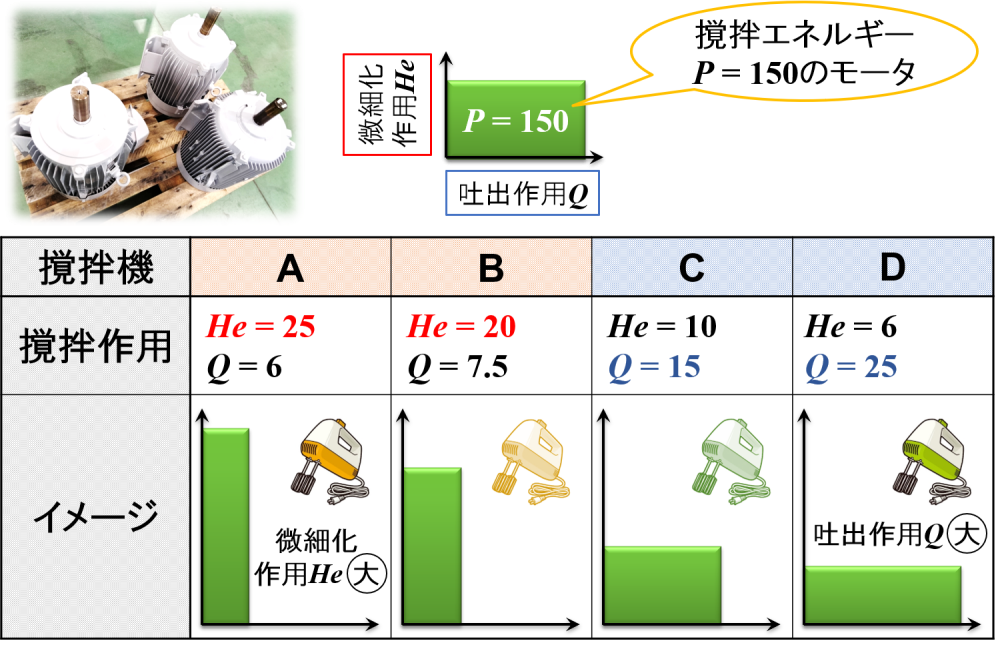
例えば下図で示すように，撹拌機によって微細化作用と吐出作用の割合が異なります。

このように，撹拌機は大きな吐出作用を発揮するものと微細化作用を発揮するものに大別されやすく，両者の撹拌作用を有効に発揮するためには，撹拌エネルギー自体を大きくするしかないと言えます。

撹拌エネルギーの式の理解

いきなり撹拌エネルギーの式を紹介しましたが，馴染みがない表現となっています。

イメージになりますが，この式の意味するところを説明したいと思います。

📝[memo]　深掘りする内容となっていますので，飛ばしても問題ありません。

まず大前提として，水動力（理論動力）の式が知られています。

これは，ポンプが単位時間に液体に与える有効エネルギーを表します。

最初に，この式の意味するところを考えます。

📝[memo]　いろいろな解釈ができますが，当社が考える内容を紹介します。

📝[memo]　式の理解を優先するため，単位は[min]ではなく[s]としています。

• 質量m = ρQt ⇒ [kg/m³]×[m³/s]×[s] = [kg]（時間tを用いる）
• 高さh = He ⇒ [m]
• 位置エネルギーP = mgh = (ρQt)×g×He = ρgHeQt ⇒ [kg]×[m/s²]×[m] = [kgm²/s²] = [J]
• 水動力（理論動力）Pw = P/t = ρgHeQ ⇒ [J]/[s] = [J/s] = [W]

このように考えると，水動力（理論動力）の式は位置エネルギーとして解釈すると理解がしやすそうです。

撹拌機とポンプはよく似ていると言われているので，この水動力（理論動力）の式を撹拌エネルギーに適用することを考えます。

ここでgHeを考えると，gHe ⇒ [m/s²]×[m] = [(m/s)²]となるので速度の2乗を意味します。

「撹拌をやさしく捉えてみよう【撹拌をどのように利用するべきか？】」のページで紹介したように，せん断力は速度の差によって変形が生じる力のことです。

せん断力がメインとなって微細化作用が発揮されるため，微細化作用はgHeで表現することができそうです。

このような解釈をすると，先述した撹拌エネルギーの式が得られます。

「スケールアップ理論を考えてみようー乳化編【周先端速度一定時における撹拌作用の変化】」のページでも，吐出作用と微細化作用の表現について取り上げることにしています。

• 吐出作用Q ⇒ [m³/s]
• 微細化作用He ⇒ [(m/s)²]
• 撹拌エネルギーP = ρHeQ ⇒ [kg/m³]×[(m/s)²]×[m³/s] = [kgm²/s³] = [W]

撹拌機とポンプの比較（撹拌作用の評価）

…というように撹拌エネルギーについて考えてきましたが，実は理由があります。

下図は，撹拌機とポンプの比較をしたものです。

撹拌機とポンプはよく似ていると言われています。

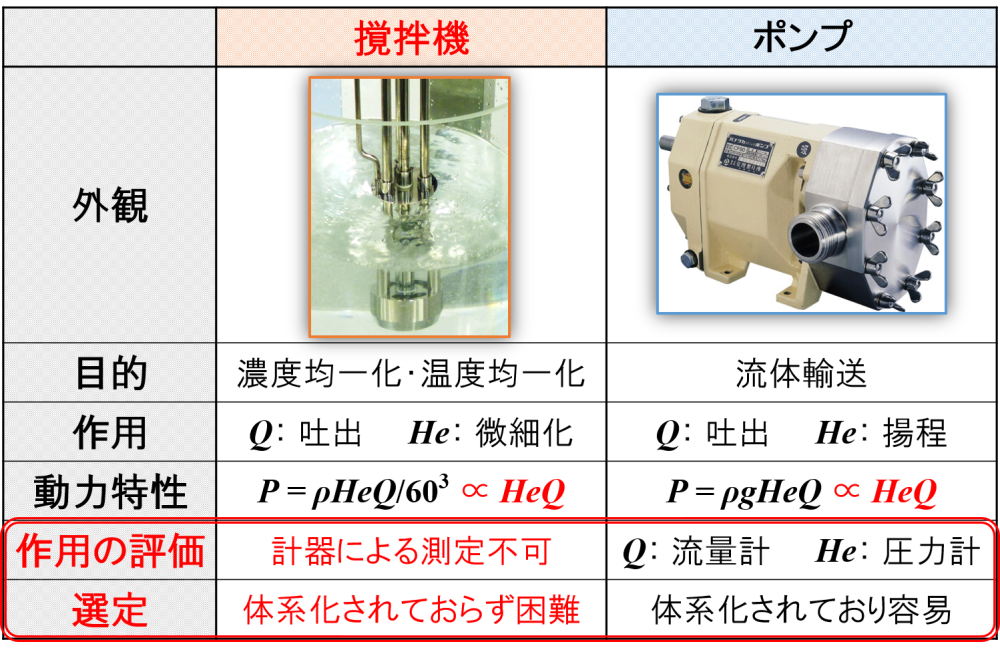
ポンプにおいても，撹拌作用に相当する「吐出量」や「揚程」がありますが，これらは計器によって測定することができます。

例えば，流量計や圧力計を使用することができます。

そのため，ポンプの能力は体系化されており，その選定は比較的容易であると考えられます。

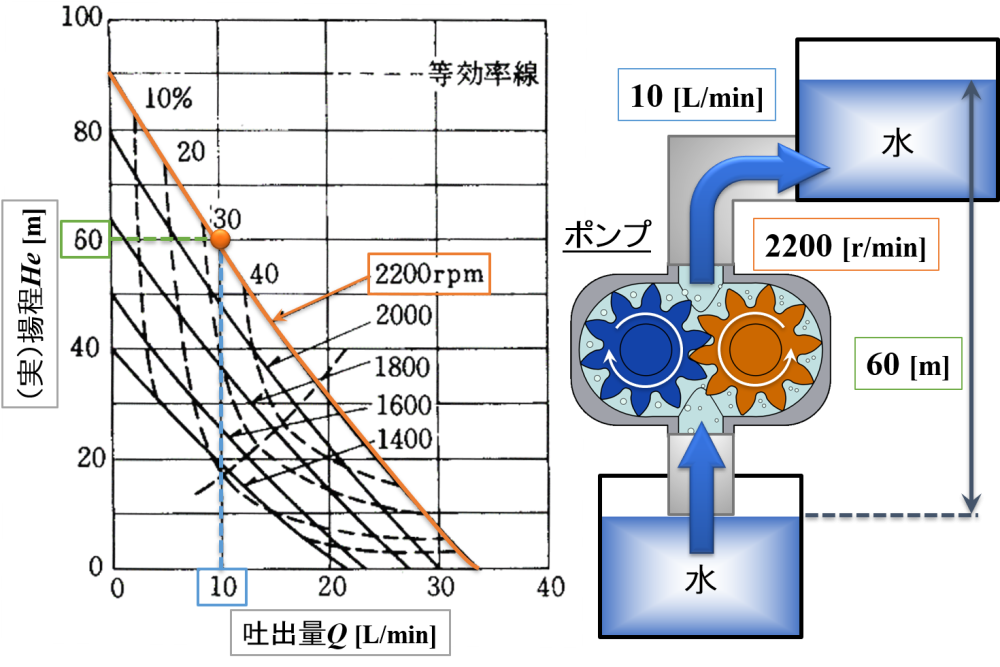
例えば，下図のような性能曲線で与えられたポンプがあるとき，2000 [r/min]で使用することを考えてみましょう。

すると，60 [m]高いところまで水を送るとき（He = 60），水量は10 [L/min]（Q = 10）であることがわかります。

🚩 [引用：化学装置百科事典編纂委員会編『化学装置百科事典』化学工業社，1971]

一方，撹拌機における撹拌作用は，計器によって測定することができないのが実情です。

すなわち，撹拌機の性能曲線が存在しません。

📝[memo]　撹拌機の吐出量のみを示したものはあるかと思います。

そのため，撹拌機の能力は撹拌作用として体系化されておらず，その選定は困難であると言えます。

このような事情を鑑みると，撹拌機としての能力を把握するために，撹拌エネルギーの多くが微細化作用と吐出作用のどちらに使用されているかを見極めることが重要になります。