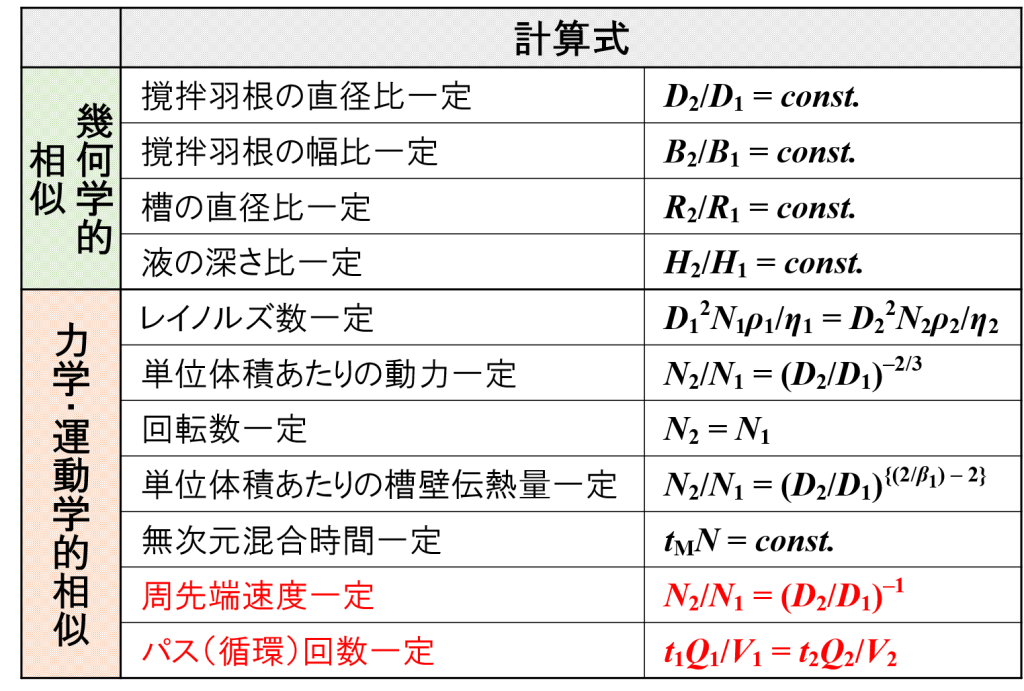
周先端速度一定時における撹拌作用の関係

「撹拌をやさしく捉えてみよう【撹拌作用の使い分け】」のページで，撹拌エネルギー（動力）P = ρHeQ/60³ ∝ HeQで表されると紹介しました。

すなわち，“微細化作用He”と“吐出作用Q”は反比例の関係にあることを意味し，“微細化作用He”と“吐出作用Q”の積は一定になります。

ここでは，“微細化作用He”と“吐出作用Q”を回転数Nとタービン羽根の直径Dで表現することを考えます。

…その前に，せん断力を考えます。

「スケールアップ理論を考えてみよう ー 乳化編【せん断力が等しくなるようにする】」のページで紹介したように，せん断力は周先端速度のみを考えれば良いという結論が得られます。

そして，「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで紹介したように，周先端速度Uは次のように表されます。

U = πND/60 ∝ ND

したがって，微細化作用Heは”ND”をベースに考えると良いことがわかります。

続いて，「スケールアップ理論を考えてみよう ー 乳化編【“ホモミキサー”による吐出量】」のページで紹介したように，吐出量Qは次のように表されます。

Q = N_qND³・10³ ∝ ND³

したがって，吐出作用Qは”ND³”をベースに考えると良いことがわかります。

一方，「撹拌をやさしく捉えてみよう【各種撹拌装置で使用する主な撹拌羽根】」のページで紹介したように，撹拌エネルギー（動力）Pは正味の所要動力P_netとして次のように表されます。

• 乱流域：P_net = K₁ρN³D⁵
• 層流域：P^*_net = K₂ηN²D³

📝[memo]　層流域で撹拌する場合は，”^*”を付して表現することにします。（層流域の事例は当分出てきませんので，ここでは無視してください。）

📝[memo]　撹拌エネルギー（動力）Pと正味の所要動力P_netは等しいと考えます。

微細化作用Heや吐出作用Qのベースとなる因子を確認できたので，特に乱流域の正味の所要動力P_netに当てはめてそれらの大きさを考えてみましょう。

すると，微細化作用と吐出作用は下記のように表現できます。

乱流域：P_net = K₁ρN³D⁵ = K₁ρ(ND)²(ND³)¹ ∝ (ND)²(ND³)¹

• 微細化作用He ∝ (ND)² = N²D²
• 吐出作用Q ∝ (ND³)¹ = ND³

微細化作用の関係

「スケールアップ理論を考えてみよう ー 乳化編【せん断力が等しくなるようにする】」のページで紹介したように，「ホモミキサーが付与するせん断力F ∝ 周先端速度U」や「液層が受けるせん断応力τ ∝ ホモミキサーが付与するせん断力F」の関係があったため，微細化作用Heは次のようにも表されます。

He ∝ N²D² ∝ (ND)² ∝ U² ∝ F² ∝ τ²

以上より，「”（条件①’）周先端速度が等しくなるようにする”という考え方」を採用することで，微細化作用Heが等しくなっていることがわかります。

📝[memo]　「He ∝ U²」が成り立ちますね。微細化作用とせん断力は比例関係にあるので，微細化作用を大きくすることはせん断力を大きくすることを意味します。

---

続いて，「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで，スケールアップ後の回転数N₂ = N₁D₁/D₂で表されると紹介しました。

ここで，スケールアップ前後の微細化作用Heを計算します。

• スケールアップ前　👉　He₁ ∝ N₁²D₁²
• スケールアップ後　👉　He₂ ∝ N₂²D₂² = {N₁²(D₁/D₂)²}・D₂² = N₁²D₁²

He₂/He₁ ∝ N₁²D₁²/N₁²D₁² = 1 (= const.)

したがって，タービン羽根の直径Dが2倍になっても，微細化作用Heは一定であることがわかります。

📝[memo]　タービン羽根の直径Dがどのような変化（どのようなスケールアップ）をしても，微細化作用Heは一定になります。

📝[memo]　当然ながら，せん断力も一定になります。

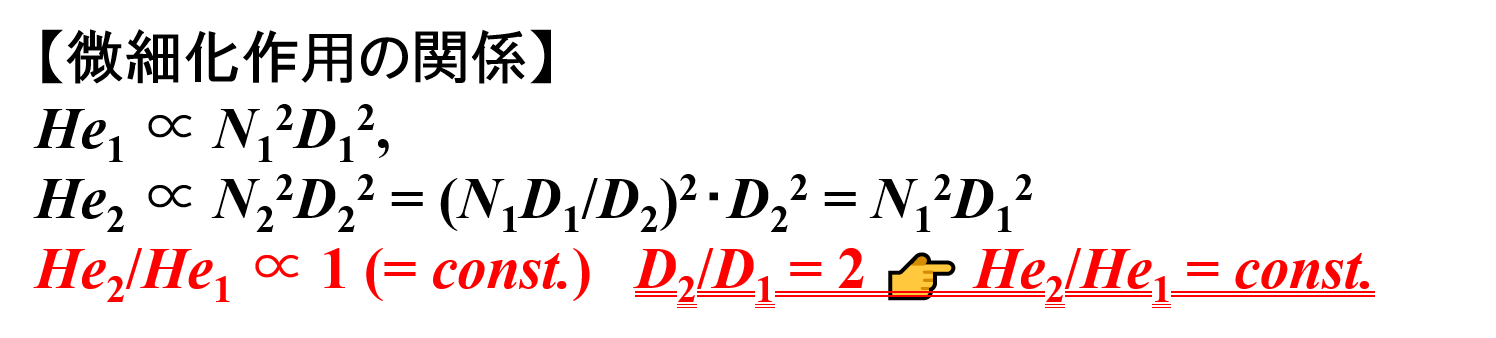
吐出作用の関係

次に，スケールアップ前後の吐出作用Qを計算します。

• スケールアップ前　👉　Q₁ ∝ N₁D₁³
• スケールアップ後　👉　Q₂ ∝ N₂D₂³ = {N₁(D₁/D₂)}・D₂³ = N₁D₁D₂²

Q₂/Q₁ ∝ N₁D₁D₂²/N₁D₁³ = (D₂/D₁)²

したがって，タービン羽根の直径Dが2倍になると，吐出作用Qは4倍になることがわかります。

📝[memo]　タービン羽根の直径Dの変化の仕方（スケールアップの仕方）によって，吐出作用Qは異なります（＝一定ではありません）。

---

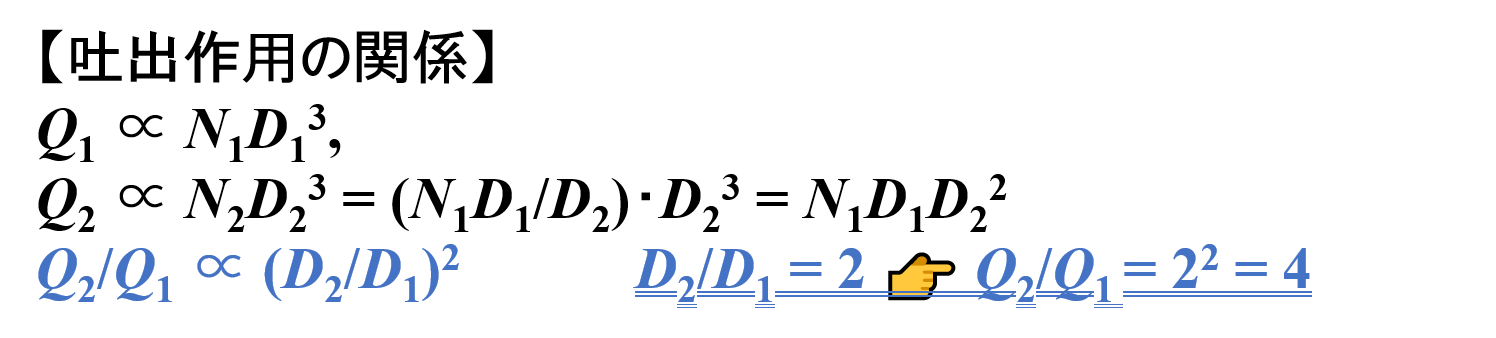
実際は吐出係数n_qが一定ではないので，吐出係数n_qを残したままスケールアップ前後の吐出作用Qを計算します。

• スケールアップ前　👉　Q₁ ∝ n_q1N₁D₁³
• スケールアップ後　👉　Q₂ ∝ n_q2N₂D₂³ = n_q2{N₁(D₁/D₂)}・D₂³ = n_q2N₁D₁D₂²

Q₂/Q₁ ∝ n_q2N₁D₁D₂²/n_q1N₁D₁³ = (n_q2/n_q1)(D₂/D₁)²

当然，吐出作用Qはタービン羽根の直径Dだけではなく，吐出係数n_qにも依存することがわかります。

ただし，吐出作用Qは吐出係数n_qよりもタービン羽根の直径Dの影響を大きく受けます。

乳化時間の関係

ここで，「スケールアップ理論を考えてみようー乳化編【パス回数が等しくなるようにする】」のページで紹介したパス回数の式について振り返ってみましょう。

そして，「”（条件②）パス回数が等しくなるようにする”という考え方」を採用して，撹拌作用ではありませんが乳化時間についても考えます。

n₂ = n₁が成り立つ条件を採用することを意味します。

• スケールアップ前　👉　t₁ ∝ n₁V₁/Q₁ ∝ n₁V₁/(N₁D₁³)
• スケールアップ後　👉　t₂ ∝ n₂V₂/Q₂ ∝ n₁V₂/(N₁D₁D₂²)

📝[memo]　パス回数の式を変形した乳化時間t = …の式に，上述した吐出量（吐出作用）Qを代入しています。

t₂/t₁ ∝ {n₁V₂/(N₁D₁D₂²)}/{n₁V₁/(N₁D₁³)} = (V₂/V₁)(D₂/D₁)^–2

したがって，タービン羽根の直径Dが2倍になると，製品仕込量Vが一定であれば乳化時間tは0.25倍になることがわかります。

📝[memo]　パス回数N_qが一定であれば，吐出量Qが4倍になるからですね。

しかしながら，スケールアップをする以上，製品仕込量Vが一定になることはありません。

「スケールアップ理論を考えてみよう ー 乳化編【相似則の利用】」のページで紹介したように，タービン羽根の直径Dとタンク径の比は一定ではありません。

すると，”タービン羽根の直径Dとタンク径の3乗に比例すると考えられる”製品仕込量V”の比も一定ではありません。

その結果，乳化時間tはタービン羽根の直径Dと製品仕込量Vによって変化するので，○○倍になるというようなきれいな結果にはなりません。

---

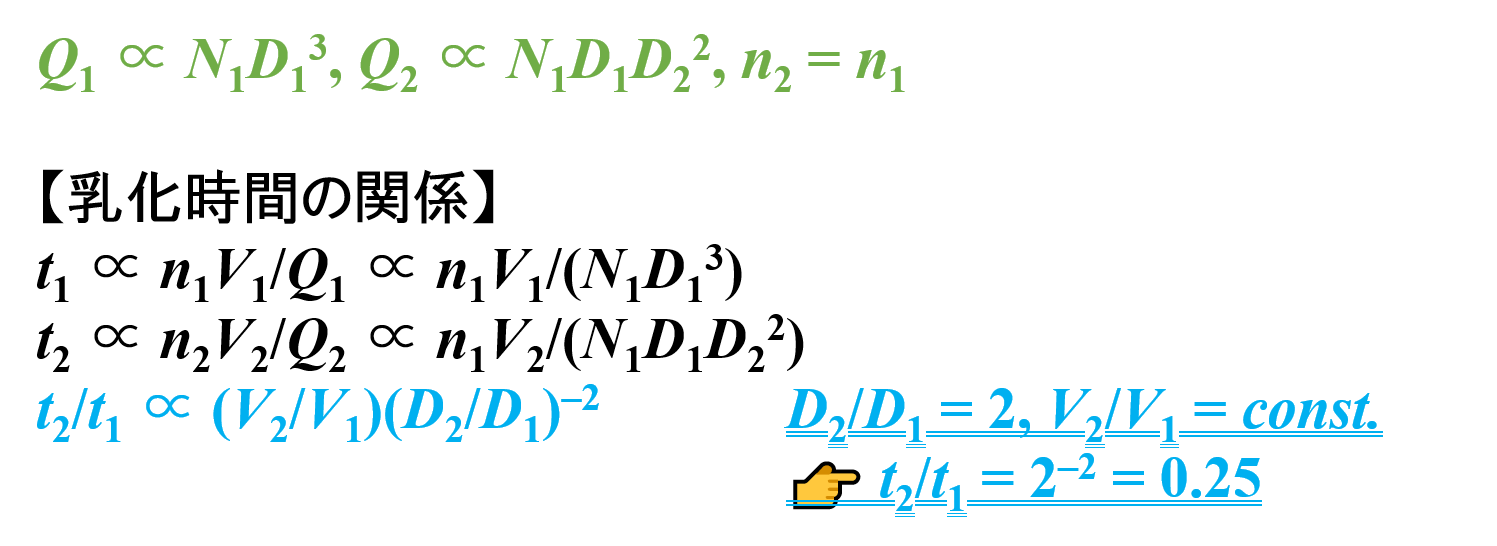
もし，タービン羽根の直径Dとタンク径の比が一定であれば，製品仕込量Vはタンク径の3乗に比例すると仮定することができます。

このとき，製品仕込量Vはタービン羽根の直径Dの3乗に比例することを意味します。

📝[memo]　比例定数をαとします。

• スケールアップ前　👉　t₁ ∝ n₁V₁/Q₁ ∝ n₁(αD₁³)/(N₁D₁³) = αn₁/N₁
• スケールアップ後　👉　t₂ ∝ n₂V₂/Q₂ ∝ n₁(αD₂³)/(N₁D₁D₂²) = αn₁/N₁・(D₂/D₁)

t₂/t₁ ∝ {αn₁/N₁・(D₂/D₁)}/(αn₁/N₁) = D₂/D₁

したがって，タービン羽根の直径Dが2倍になると，乳化時間tは2倍になることがわかります。

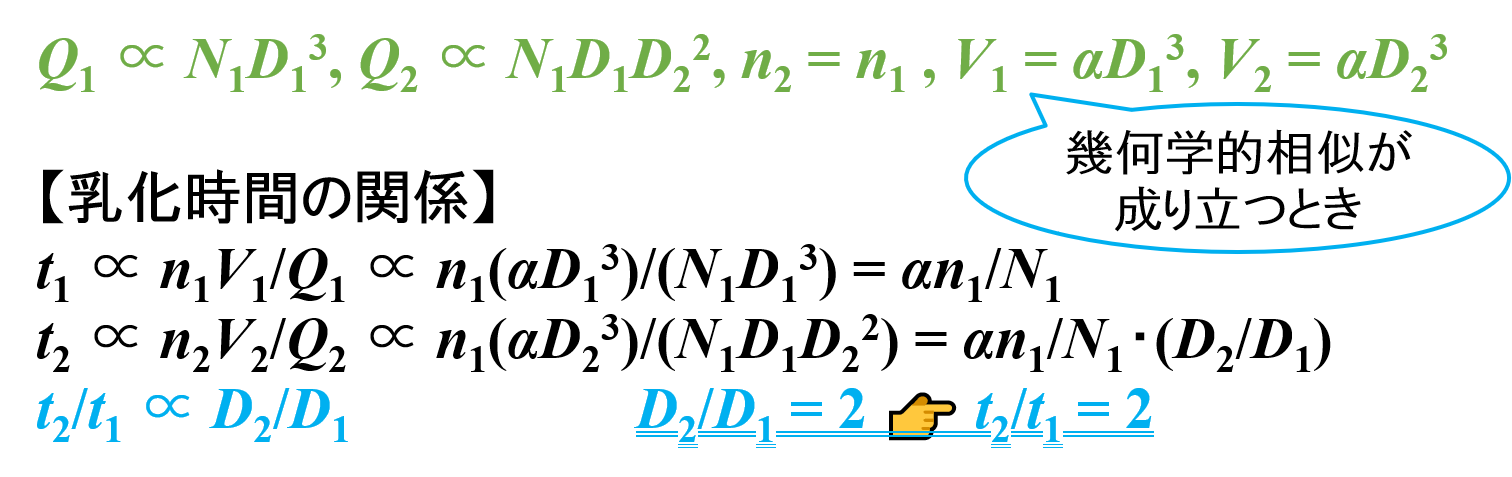
まとめ

ここで，まとめをしておきましょう。

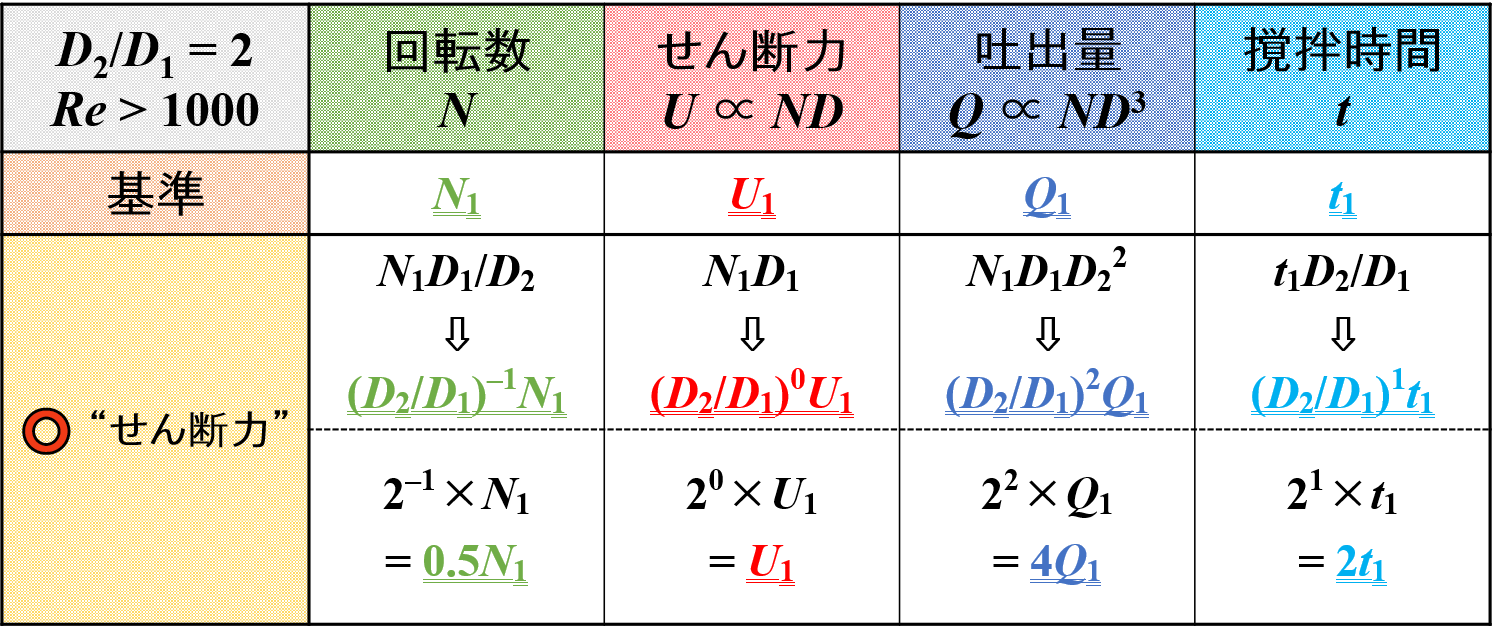
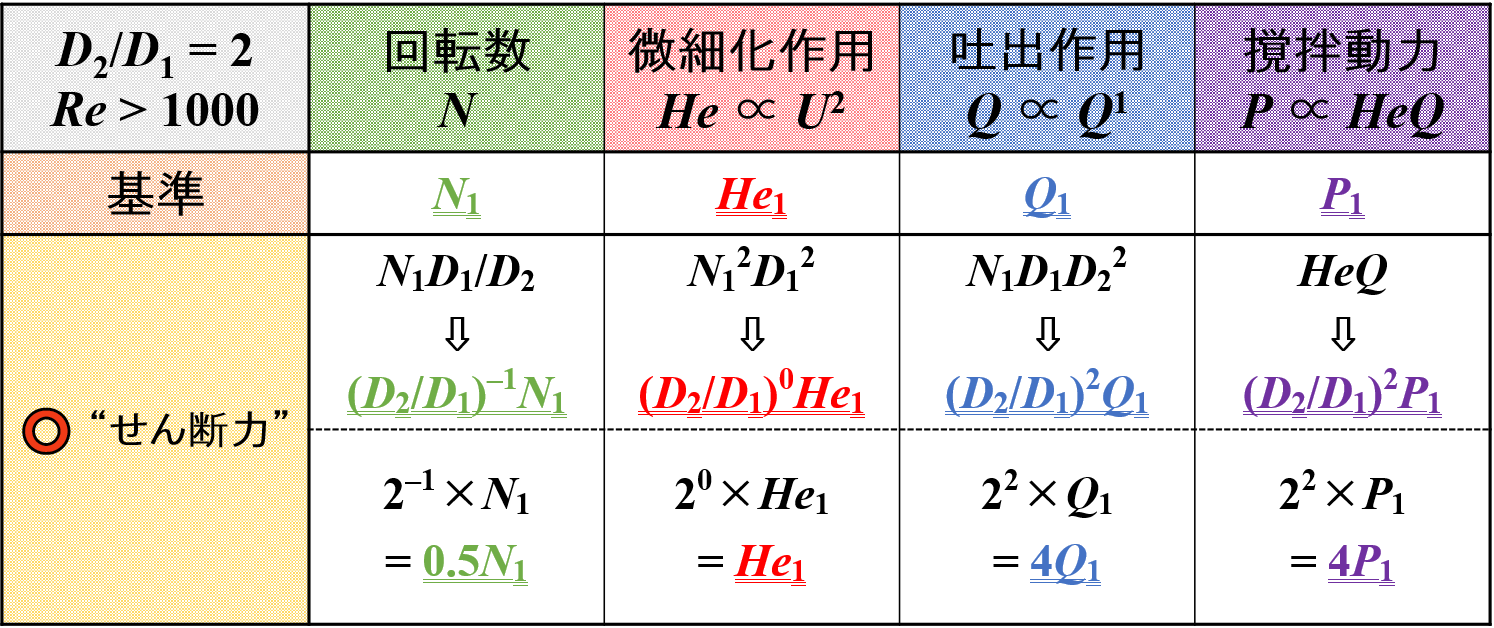
スケールアップをして羽根径が2倍になると，周先端速度一定時において各種因子は下表のように変化します。

“高速撹拌機”の機械的な力の評価

ここで，機械的な力について整理をしておきましょう。

「スケールアップでエマルションを評価しよう【スケールアップの考え方】」のページで紹介したように，スケールアップは「規模」を変更する操作を意味しているので，この”処方的な力”は，通常，変更することはありません。

一方，使用する撹拌装置が変わったとしても“機械的な力”を等しく与えることができれば，”機械的な力”はスケールアップ前後で変化しないと言えます。

その結果，スケールアップ前後で”処方的な力”と”機械的な力”は変化しない（＝等しい・同じ）という状況を作り出すことができます。

そこで，「スケールアップ理論を考えてみよう ー 乳化編【ホモミキサーによる微細化作用とスケールアップ計算式】」のページでは，ホモミキサーの具体的な撹拌条件を決めることを考えました。

この考え方に基づくと，最終的に生成する液滴の大きさ・分布が等しくなるので，結果的に”機械的な力”が等しい！と判断しました。

しかしながら，周先端速度一定時における撹拌作用の関係を調べてみると，厳密にはスケールアップ前後で微細化作用Heのみが一定になることがわかりました。

スケールアップ前後で吐出作用Qは変化してしまいます。

“機械的な力”を等しく与えることを目指してきましたが，実際にはスケールアップ前後で“微細化作用He”と“吐出作用Q”を共に等しくすることはできません。

ただし，乳化時間tで調整してパス回数nが等しくなるようにしているので，“吐出作用Q”に対して補正を加えているようなイメージです。

正確には“機械的な力”である“微細化作用He”を等しくすることで，（吐出作用Qは等しくないけれど）”機械的な力”を等しいとみなすことができるだろう！というのが，ここでの提案になります。

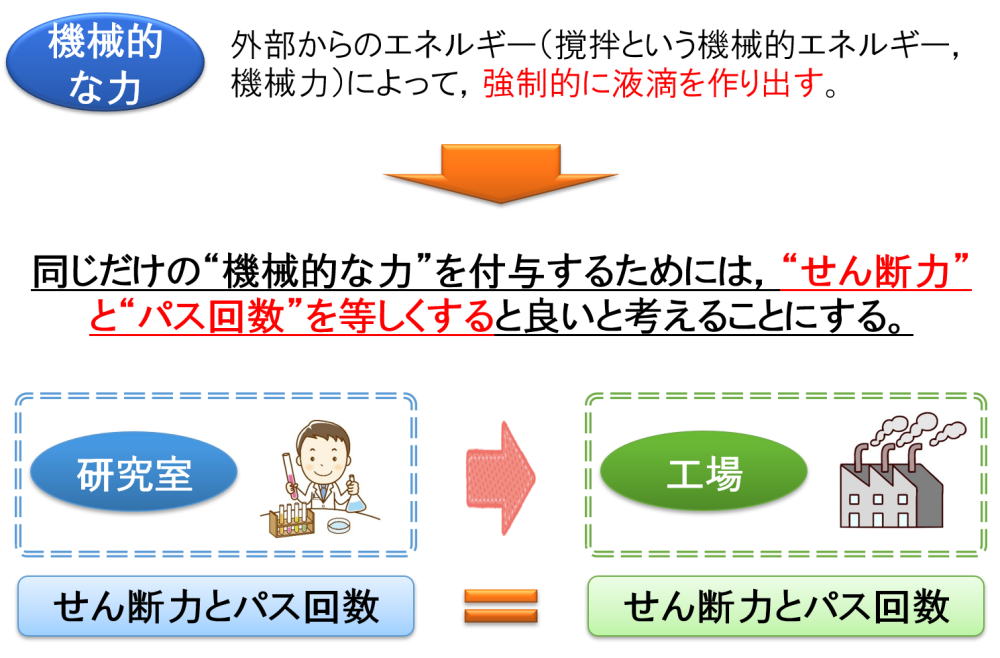
”スケールアップの考え方”の整理⑶

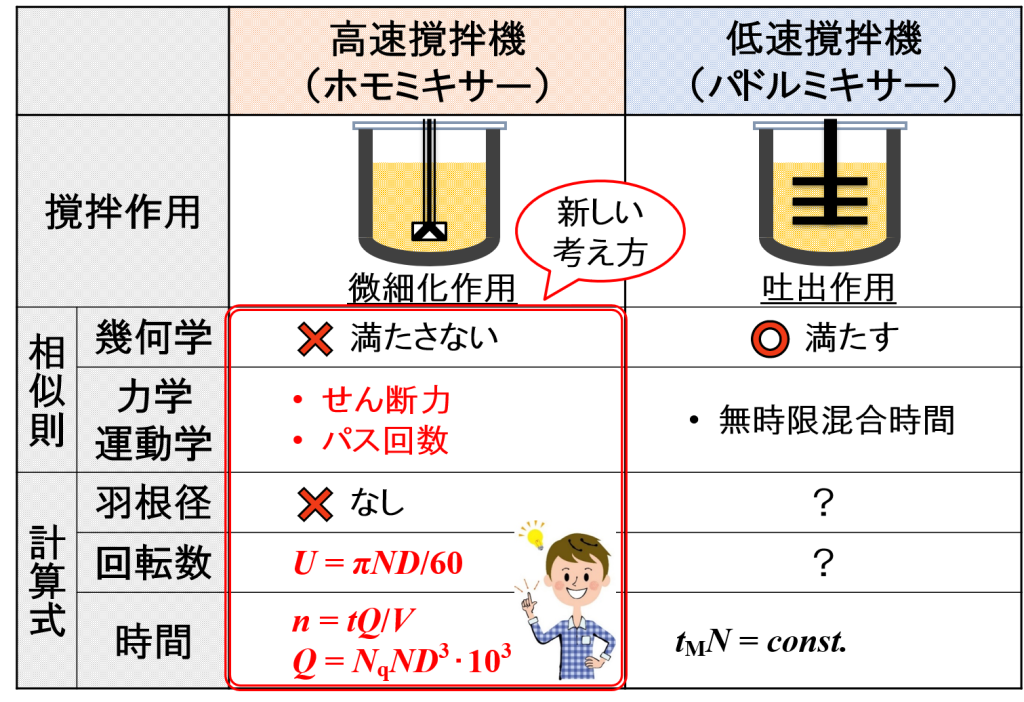
「スケールアップ理論を考えてみようー乳化編【相似則の利用】」のページで，表を作成しました。

そして，高速撹拌機における力学・運動学的相似は，せん断力とパス回数について考えました。

これは，低速撹拌機にはない考え方と言えます。

以上の考え方をまとめると，下図のように表すことができます。

現段階で説明していない箇所は”？”としています。

“相似則”の関係を採用すると，様々な考え方からスケールアップの計算式が成り立っています。

高速撹拌機であるホモミキサーでは，下表で示す2つの計算式（赤字）を採用することになります。