”スケールアップの考え方”の整理⑷

「スケールアップ理論を考えてみようー乳化編【周先端速度一定時における撹拌作用の変化】」のページで述べた内容と同じですが，一旦整理をしておきましょう。

これまでは，高速撹拌機（ホモミキサー）を中心に考えてきました。

今度は，低速撹拌機（パドルミキサー）について着目し，スケールアップを考えていきます。

ただ，「Introduction【全体イメージ】」のページで述べたように，低速撹拌機は世の中で言うところの一般的な撹拌機に該当します。

そのため，完ぺきとは言えませんが，ある程度理論体系が出来上がっています。

当社は高速撹拌機を主力とするメーカーであり，低速撹拌機に関する理論は専門外のところがあります。

厳密な理解や詳細な内容は関連する専門書へ譲るとして，ここではイメージや考え方を紹介します。

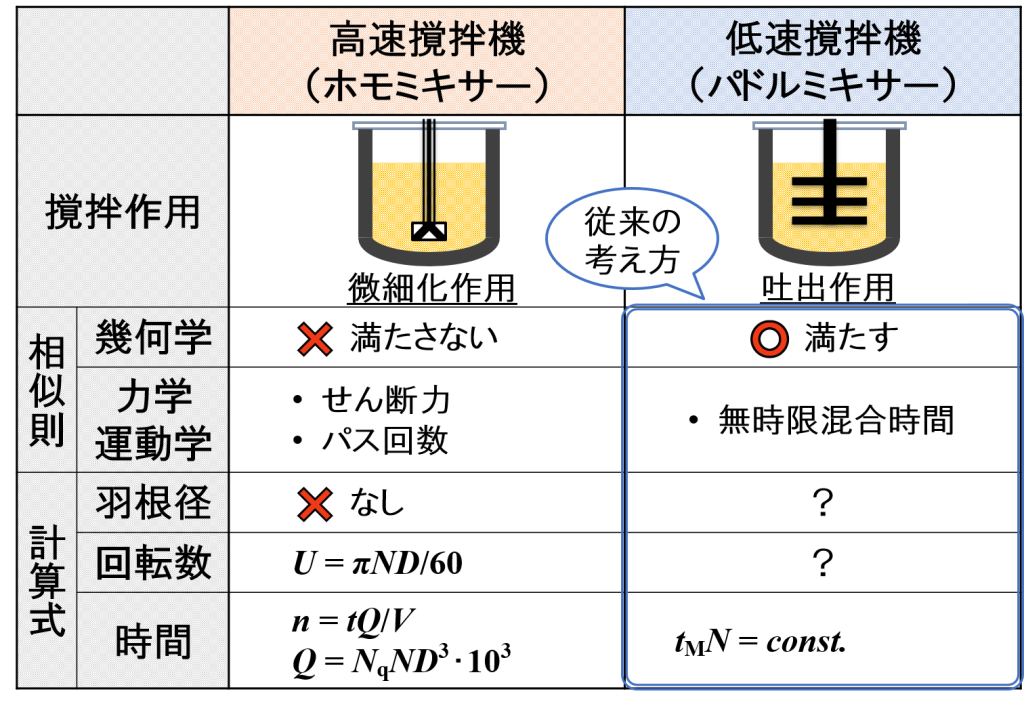
“液体”＋“液体”の一般的な撹拌（パドルミキサー）の場合

「スケールアップ理論を考えてみよう ー 乳化編【ホモミキサーによる微細化作用とスケールアップ計算式】」のページで紹介したホモミキサーの場合と似ていますが，当然，異なる点があります。

それは，液滴の微細化と合一を繰り返すことです。

📝[memo]　乳化を想定した場合は，液滴の微細化が起こり，小さくなった液滴はそのまま存在すると考えました。

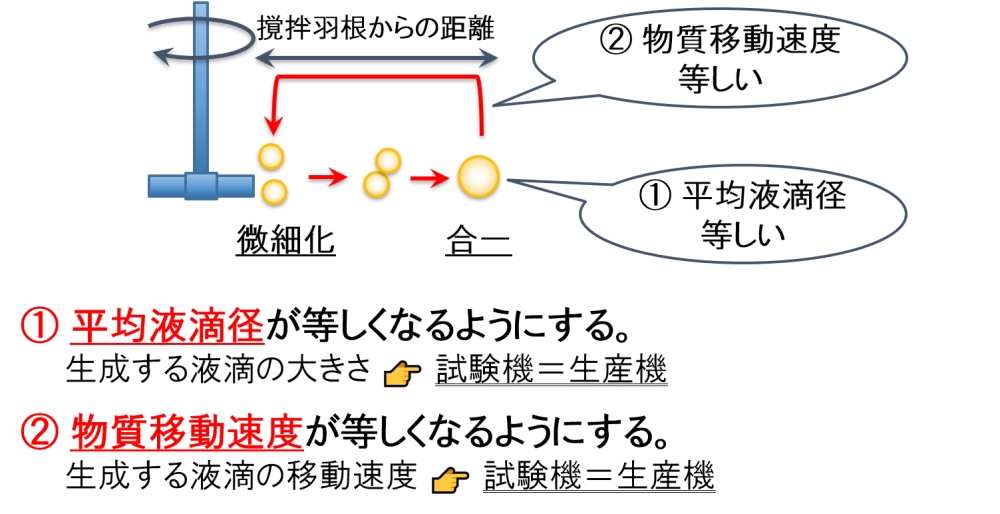
そこで，スケールアップをするにあたって，次の2つの条件が成り立つような設定をすることを考えます。

① 平均液滴径が等しくなるようにする。

試験機で使用するパドルミキサーと生産機で使用するパドルミキサーによって生成する液滴の大きさが，どちらも等しくなるように設定します。

液滴の微細化と合一を繰り返すため，このときの液滴の平均液滴径を等しくすることを考えます。

② 物質移動速度が等しくなるようにする。

試験機で使用するパドルミキサーと生産機で使用するパドルミキサーによって生成する物質移動速度が，どちらも等しくなるように設定します。

合一した液滴が再び微細化されるような，液滴の移動速度を等しくすることを考えます。

上述した2つの条件をまとめると，_①大きさが等しい液滴が_②同じ速度で移動すると，同じ混合状態が得られると考えることができます。

その結果，スケールアップ前後（研究室と工場）における”機械的な力”を等しくすることができるだろう！というのが，一般的な撹拌機におけるスケールアップの基本的な考え方になります。

（条件①）平均液滴径が等しくなるようにする

厳密な理解や詳細な内容は関連する専門書へと譲るとして，平均液滴径に関して下式が明らかになっているとします。

そして，面積体積平均粒子径d₃₂をパドルミキサーの直径（羽根径）Dで割ったものを平均液滴径d₃₂/Dとみなし，スケールアップ前後でこれを等しくなるようにすることを考えます。

面積体積平均粒子径d₃₂とは…

先に，面積体積平均粒子径d₃₂について簡単に触れておきます。

平均液滴径を考える際，面積体積平均粒子径d₃₂を採用する理由は，界面の影響が大きい表面積に重きを置くためと考えているようです。

次に，面積体積平均粒子径d₃₂の導出をしておきます。

総体積

V_p = Σ(4/3)π(d/2)³ = Σπd³/6

総表面積

A_p = Σ4π(d/2)² = Σπd²

総体積/総表面積

V_p/A_p = (Σπd³/6)/Σπd² = (1/6)・(Σd³/Σd²) = (1/6)・d₃₂

⇔ d₃₂ = 6V_p/A_p = 6(Σπd³)/(Σπd²)

撹拌ウェーバー数Weとは…

続いて，撹拌ウェーバー数Weについても簡単に触れておきます。

「撹拌ウェーバー数＝慣性力/表面張力」で定義されるので，撹拌機による微細化作用＝慣性力，液滴が微細化されないように耐える力＝表面張力とイメージすることができます。

したがって，撹拌ウェーバー数は，撹拌による微細な液滴生成のしやすさを示す指標と捉えることができそうです。

次に，撹拌ウェーバー数Weの導出をしておきます。

慣性力

F_i = ma = ρD³(dU/dt)

📝[memo]　運動方程式を想定しています。力F = 物体の質量m × 加速度a

ここで，U = dU，dt = D/Uとすると，

F_i = ρD³(dU/dt) = ρD³{U/(D/U)} = ρD²U²

📝[memo]　「時間＝距離（長さ）/速度」となるように，長さを表す単位である羽根径Dを使用して時間を表しています。

表面張力（絶対値としての力）

F_s = γD

📝[memo]　「撹拌の立場から乳化をイメージしよう【界面自由エネルギーの考え方】」のページで，界面自由エネルギーの式を紹介しました。

📝[memo]　「力＝界面張力（表面張力）×長さ」となるように，長さを表す単位である羽根径Dを使用して時間を表しています。

撹拌ウェーバー数（＝慣性力/表面張力）

We = F_i/F_s = ρD²U²/γD = ρDU²/γ

ここで，U = NDなので，

We = ρDU²/γ = ρD(ND)²/γ = ρN²D³/γ

📝[memo]　定数項（π/60）を無視して，周先端速度Uを採用しています。

平均液滴径d₃₂/Dを決める因子

平均液滴径d₃₂/Dは，パドルミキサーの直径（羽根径）D，係数C’とC”，分散相の体積分率Φ，撹拌ウェーバー数Weによって決まります。

処方が変わらないのであれば，混合をするときの分散液の物性はスケールに関係なく同じであるはずです。

したがって，係数C’とC”，分散相の体積分率Φは常に一定でありスケールアップ前後で変化しません。

また，使用するパドルミキサーが決まっているので，パドルミキサーの直径（羽根径）Dは自然に決定する値で定数です。

ということは，平均液滴径d₃₂/Dがスケールアップ前後で等しくなるようにするためには，面積体積平均粒子径d₃₂が等しくなれば良いという結論が得られます。

📝[memo]　平均液滴径d₃₂/Dを考えるとき，パドルミキサーの直径（羽根径）Dが一定であれば，変数である面積体積平均粒子径d₃₂だけを考えれば良いですよね。

すなわち，「”（条件①）平均液滴径が等しくなるようにする”という考え方」＝「”（条件①’）面積体積平均粒子径が等しくなるようにする”という考え方」であることがわかります。

次に，面積体積平均粒子径d₃₂がどのような式の形で表現できるか？を確認してみましょう。

d₃₂/D ∝ We^–0.6 ⇔　d₃₂ ∝ We^–0.6D = (ρN²D³/γ)^–0.6D = (ρ/γ)^–0.6(N³D²)^–0.4

ここで，密度ρと界面張力γはスケールアップ前後で変化しません。

d₃₂ ∝ (N³D²)^–0.4

すなわち，「”（条件①’）面積体積平均粒子径が等しくなるようにする”という考え方」＝「”（条件①”）N³D²が等しくなるようにする”という考え方」であることがわかります。

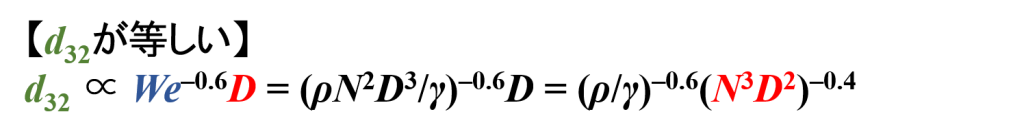
（条件②）物質移動速度が等しくなるようにする

同じく，厳密な理解や詳細な内容は関連する専門書へ譲るとして，物質移動速度に関して下式が明らかになっているとします。

そして，スケールアップ前後で物質移動速度を等しくなるようにすることを考えます。

物質移動速度dC/dtを決める因子

物質移動速度dC/dtは，係数k，分散相の体積分率Φ，溶質の飽和濃度C*，溶質の濃度C，面積体積平均粒子径d₃₂によって決まります。

処方が変わらないのであれば，混合をするときの分散液の物性はスケールに関係なく同じであるはずです。

したがって，係数k，分散相の体積分率Φ，溶質の飽和濃度C*，溶質の濃度Cは常に一定でありスケールアップ前後で変化しません。

ということは，物質移動速度dC/dtがスケールアップ前後で等しくなるようにするためには，面積体積平均粒子径d₃₂が等しくなれば良いという結論が得られます。

すなわち，「”（条件②）物質移動速度が等しくなるようにする”という考え方」＝「”（条件①’）面積体積平均粒子径が等しくなるようにする”という考え方」であることがわかります。

これ以降の考え方は，上述した内容と全く同じです。

すなわち，「”（条件①’）面積体積平均粒子径が等しくなるようにする”という考え方」＝「”（条件①”）N³D²が等しくなるようにする”という考え方」であることがわかります。

（条件①”）N³D²が等しくなるようにする”という考え方

“液体”＋“液体”の一般的な撹拌（パドルミキサー）の場合，次の2つの条件が成り立つような設定をすることを考えました。

• （条件①）平均液滴径が等しくなるようにする
• （条件②）物質移動速度が等しくなるようにする

しかしながら，2つの条件が成り立つような設定をして考えてきたのですが，同じ結論が得られることがわかりました。

このとき登場した”N³D²”は何を意味するのか？というのが，次のテーマになります。

合一を無視できる場合

参考までに，おまけの話をしておきたいと思います。

本題は，最終的に”N³D²”が登場するというところで終わっています。

これまでのモデルは，撹拌によって液滴の微細化と合一を繰り返すことでした。

このとき，平均液滴径に関して下式が明らかになっていました。

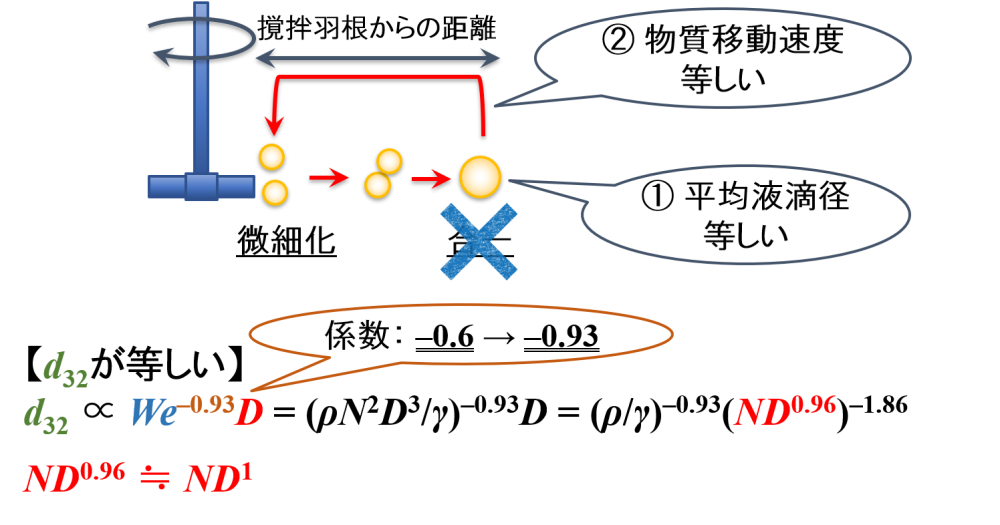
一方で，乳化を想定した場合は，液滴の微細化後に合一は引き起こされないと考えました。

再び，平均液滴径に関する式に着目すると，撹拌ウェーバー数Weの指数が”–0.93”で表すことができるという実験事実があるようです。

📝[memo]　引用文献です。「Konno, M. and S. Saito : J. Chem. Eng. Jpn., 20, 533-535 (1987)」

平均液滴径d₃₂/Dがスケールアップ前後で等しくなるようにするためには，面積体積平均粒子径d₃₂が等しくなれば良いという結論が得られました。

そこで，撹拌ウェーバー数Weの指数が”–0.93”で表すことができるとき，面積体積平均粒子径d₃₂がどのような式の形で表現できるか？を確認してみましょう。

d₃₂/D ∝ We^–0.93 ⇔　d₃₂ ∝ We^–0.93D = (ρN²D³/γ)^–0.93D = (ρ/γ)^–0.93(ND^0.96)^–1.86

ここで，密度ρと界面張力γはスケールアップ前後で変化しません。

d₃₂ ∝ (ND^0.96)^–1.86

すなわち，「”（条件①’）面積体積平均粒子径が等しくなるようにする”という考え方」＝「”（条件③）ND^0.96が等しくなるようにする”という考え方」であることがわかります。

このとき，「ND^0.96 ≒ ND¹」であるので，「”（条件③’）NDが等しくなるようにする”という考え方」に置き換えます。

d₃₂ ∝ (ND)^–1.86

そして，このとき登場した”ND”は何を意味するのか？ということを考えます。

すると，「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで紹介した”周先端速度”であることがわかります。

📝[memo]　π/60は常に一定なので，周先端速度Uは”ND”によって決まります。

したがって，乳化を想定したスケールアップを考えた場合，異なるアプローチからであっても周先端速度のみを考えれば良いという結論が得られます。