周先端速度の式

「スケールアップ理論を考えてみよう ー 乳化編【せん断力が等しくなるようにする】」のページで紹介したように，せん断力を周先端速度に置き換えることができました。

その結果，「スケールアップ理論を考えてみよう ー 乳化編【ホモミキサーによる微細化作用とスケールアップ計算式】」で紹介した”（条件①）せん断力が等しくなるようにする”の考え方と同じになりました。

すなわち，「”（条件①）せん断力が等しくなるようにする”という考え方」＝「”（条件①’）周先端速度が等しくなるようにする”という考え方」であることがわかります。

周先端速度の意味

周先端速度とは，言葉通り「周先端」における「速度」を言います。

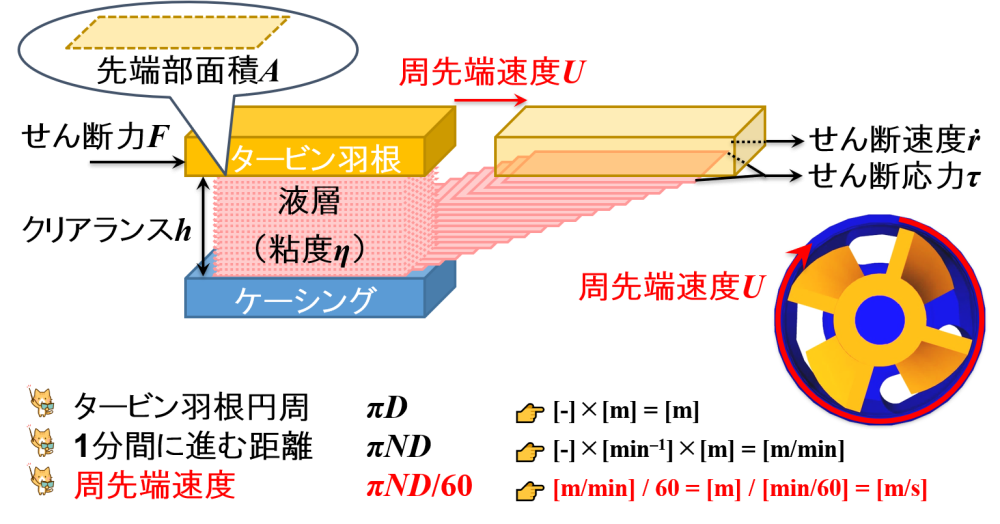
ここで，式の成り立ちについて簡単に確認しておきます。

タービン羽根円周 πD　👉　[-]×[m] = [m]

円周を求める公式そのものです。

1分間に進む距離 πND　👉　[-]×[min^–1]×[m] = [m/min]

1分間に回転する回数が回転数です。

そのため，1分間に進む距離は「タービン羽根円周」×「回転数」で得られます。

周先端速度 πND/60　👉　[m/min] / 60 = [m] / [min/60] = [m/s]

1秒間に進む距離を求めるために，単位換算をします。

周先端速度を決める因子

次に，周先端速度の式に着目します。

周先端速度Uは，円周率π，回転数N，タービン羽根の直径Dによって決まります。

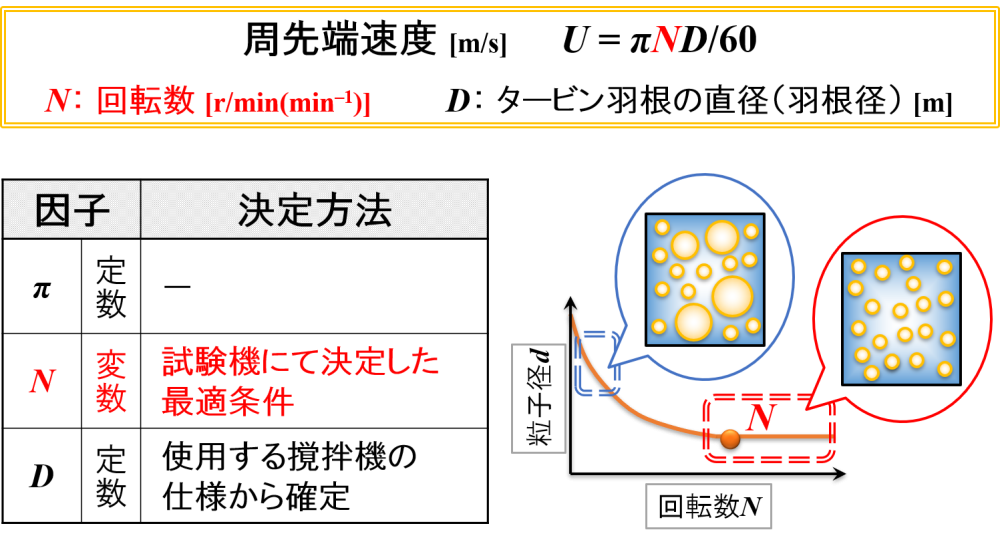
円周率π　👉　定数

あえて円周率πを含めましたが，ご存じの通り円周率π（=3.14…）は定数です。

回転数N　👉　変数

試験機にて決定した最適条件によって決まるものです。

回転数Nと粒子径dの関係を調べ，これ以上回転数Nを高くしても粒子径dが小さくならない値を調べます。

タービン羽根の直径D　👉　定数

使用するホモミキサーが決まっているので，自然に決定する値です。

このように考えると，最適な回転数Nさえ決めてしまえば，周先端速度Uは計算によって求められることがわかります。

📝[memo]　円周率πとタービン羽根の直径Dは決まった値を持っているので，変えることはできません。

周先端速度の式を使用することで，“せん断力F（＝周先端速度U）が等しくなるようにする”条件から，生産機における最適な回転数Nを求めることができます。

具体的な計算については，「スケールアップ理論を考えてみよう ー 乳化編【スケールアップの検討例①】」のページで紹介します。

“周先端速度一定”の一般式としての表し方

一般的に，「N₂/N₁ = (D₂/D₁)^–1」と表されることがあります。

下図に記載されているような計算をすることによって，最終的に上記の結論が得られます。

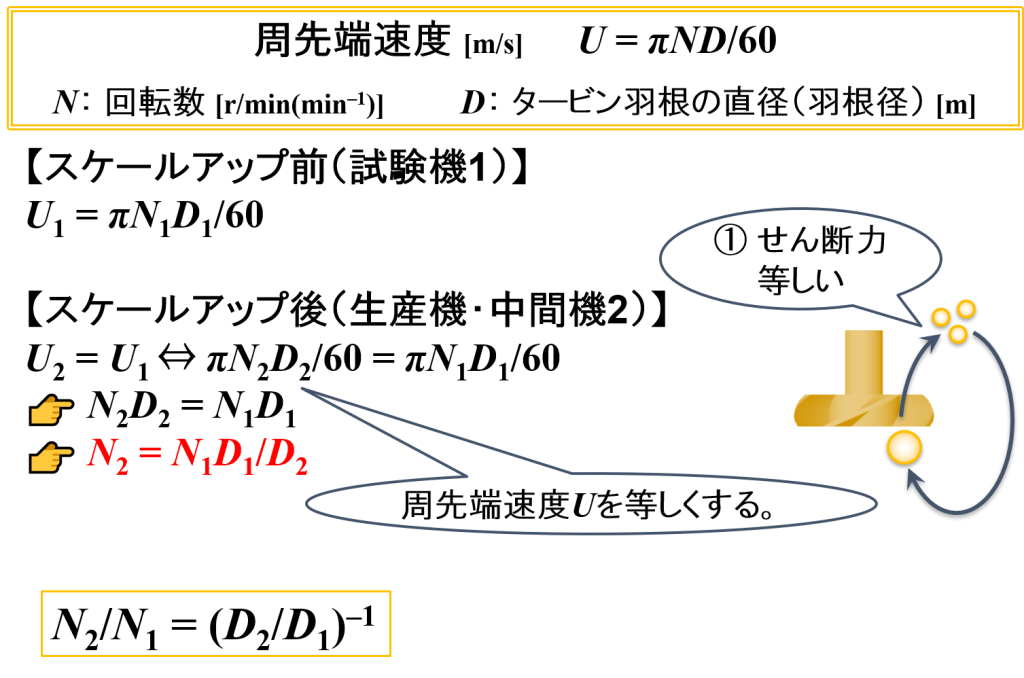
スケールアップ前

このときの回転数N₁，タービン羽根の直径D₁とすると，周先端速度は「U₁ = πN₁D₁/60」となります。

スケールアップ後

このときの回転数N₂，タービン羽根の直径D₂とすると，周先端速度は「U₂ = πN₂D₂/60」となります。

“周先端速度一定”であるため，「U₂ = U₁」となります。

そして，式変形をしていくと「N₂ = N₁D₁/D₂」となります。

回転数Nを左辺，タービン羽根の直径Dを右辺に移項すると「N₂/N₁ = (D₂/D₁)^–1」が得られます。

📝[memo]　U₂ = U₁　⇔　πN₂D₂/60 = πN₁D₁/60　⇔　N₂D₂ = N₁D₁　⇔　N₂ = N₁D₁/D₂　⇔　N₂/N₁ = (D₂/D₁)^–1

ディスパーミキサーの場合

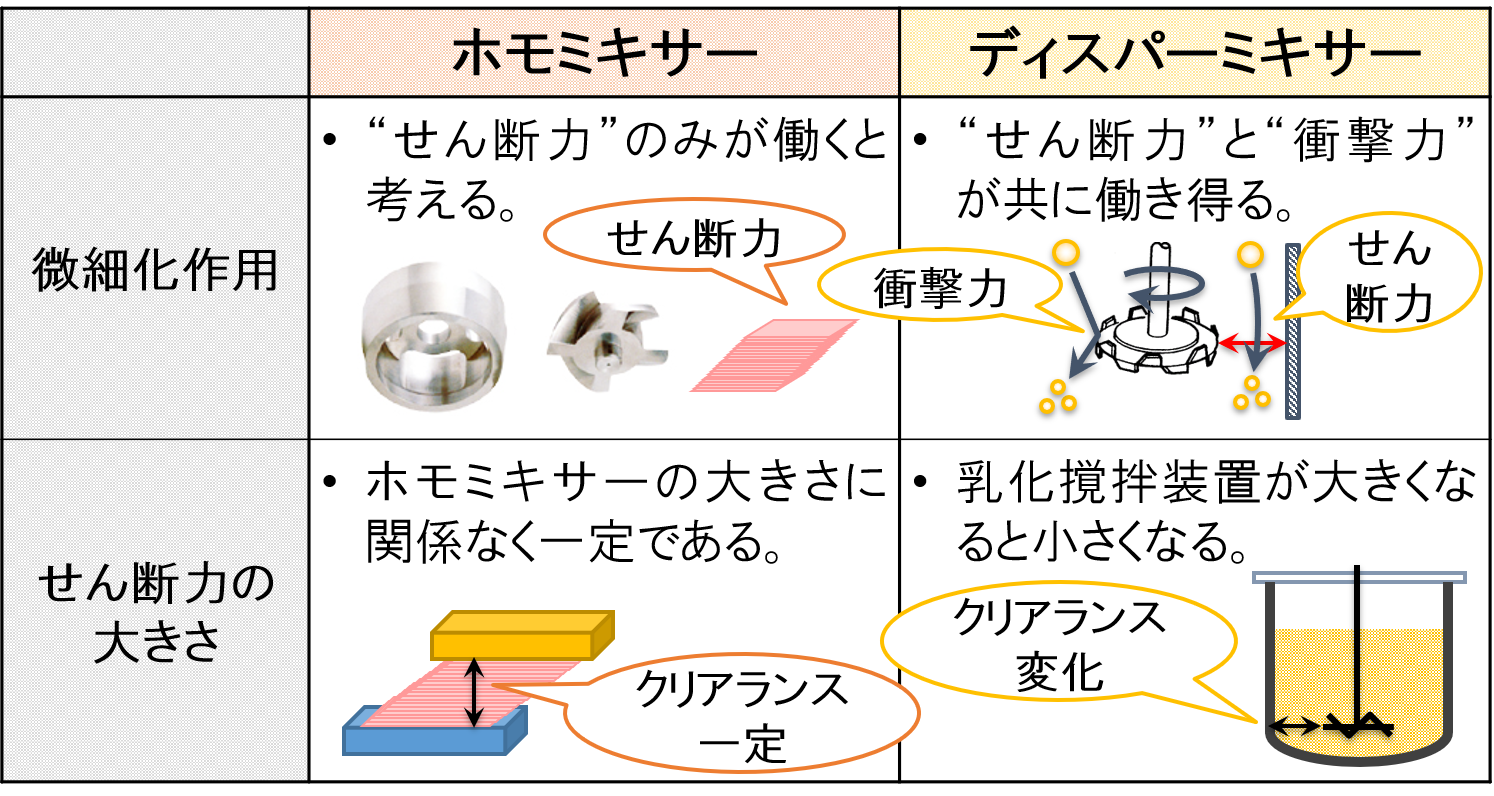
ディスパーミキサーにおける微細化作用を考えると，ホモミキサーより複雑になります。

…というのも，ディスパーミキサーではせん断力と衝撃力を発揮すると考えられるためです。

ディスパーミキサーの微細化作用に関しては当社以外で多くの研究がなされているかと思いますので，詳細な説明はお任せしたいと思います。

ここでは，ディスパーミキサーのスケールアップに関する当社独自の考え方を紹介します。

衝撃力

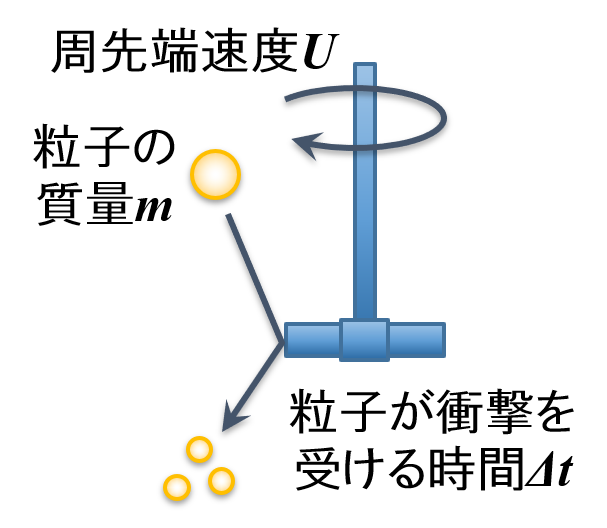
せん断力については周先端速度の式が使用できるとして，衝撃力については次式で表現できると仮定します。

📝[memo]　運動量ｍUを持つある物体が衝突し，時間Δtだけ受けて運動量が0になったとしたときの力Fを衝撃力と仮定します。（「力積FΔt＝運動量mU」の考え方）

📝[memo]　ここではある粒子がディスパーミキサーによって衝撃力Fを時間Δtだけ受けて，質量mの粒子がディスパーミキサーの周先端速度Uで動き出したというモデルを想定します。

ここで，「スケールアップ理論を考えてみよう ー 乳化編【せん断力が等しくなるようにする】」のページで考えたように，スケールアップの目的でディスパーミキサーを使用すると自然に守られる2つの条件について考えます。

粒子の質量m

通常，固体粒子を分散をするときディスパーミキサーを使用します。

処方が変わらないのであれば，分散をするときの分散液の物性はスケールに関係なく同じであるはずです。

したがって，粒子の質量mは常に一定でありスケールアップ前後で変化しません。

粒子が衝撃を受ける時間Δt

粒子の質量mは変わらないことに加えて，ディスパーミキサー近傍における粒子の移動速度は0と仮定します。

このような仮定が成り立つのであれば，粒子が衝撃を受ける時間Δtは常に一定でありスケールアップ前後で変化しません。

ここで，「F = mU/Δt」の式に着目すると，「スケールアップ前後で変化しない値」＝「粒子の質量m，粒子が衝撃を受ける時間Δt」は無視することができるため，「F ∝ U」とみなすことができます。

すなわち，衝撃力Fは周先端速度Uのみを考えれば良いという結論が得られます。

ただし，「粒子の質量m，粒子が衝撃を受ける時間Δt」は本当に無視することができると言って良いのか？という問題が付きまといます。

確信はないので，あくまでも参考値という意味合いが強くなりそうです。

せん断力

せん断力については，ホモミキサーと同様の考え方をします。

ディスパーミキサーの場合，クリアランスhはディスパーミキサー先端とタンク壁面との間を意味します。

そのため，「スケールアップ理論を考えてみよう ー 乳化編【せん断力が等しくなるようにする】」のページで述べたクリアランスhが一定にならないという問題があります。

ただ，周先端速度の式を使わざるを得ないので，無理矢理計算をすることになります。

ディスパーミキサーによるスケールアップ手法

このように考えてみると，ディスパーミキサーのスケールアップは理論計算が難しいことがわかります。

すなわち，無理矢理計算はできるけど計算結果が理論的に正しいとは言えず，あくまでも参考値になってしまします。

そこで，ホモミキサーによるスケールアップ計算で目安となる回転数を求め，生産機による実証を行い見極めることが重要になります。

ディスパーミキサーは，ホモミキサーと比べてメジャーな撹拌羽根と言えます。

乳化目的とは限りませんが，ディスパーミキサーを採用するメーカーは多いかと思います。

ここでは，ホモミキサーと同じスケールアップ理論を適用すると難しいことが多いですよ！というところで終わりたいと思います。

📝[memo]　「スケールアップ理論を考えてみよう ー 乳化編【“N^3D^2”とは？】」のページで紹介するスケールアップ理論（単位体積あたりの動力一定）を使用することが一般的かもしれません。