ホモミキサーによるトルク

ここからは，少しおまけのような話となります。

ホモミキサーを使用して流体を動かすことを考えたとき，必要なトルクや仕事を理論計算したいと思います。

理化学辞典によると，「固定軸のまわりの剛体の回転では，剛体の各部分に働く力の固定軸のまわりのモーメントだけが有効であり，これをその軸まわりのトルクと言う」と書かれています。

このままでは難しい表現なので，「ある物体を回転させるための能力」と理解することにします。

そして，「物体」＝「流体」と置き換えて，ホモミキサーによるトルクを考えます。

トルク

一般に，トルクは「物体に加わる力」と「回転の軸からみた力の加わる点までの距離」の積で表される量です。

物体＝流体と置き換えるので，「”流体”に加わる力F_H」を考えることになります。

これは，「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで紹介したように，「”流体”に加わる力F_H」が慣性力になると考えることができます。

この慣性力が粘性力を上回ることができれば，流体は自由に動くことができます。

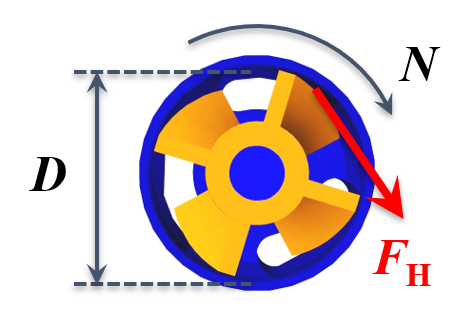
また，回転の軸からみた力の加わる点までの距離＝羽根径の半分（半径）と置き換えることができます。

したがって，「羽根径の半分（半径）D/2」を考えることになります。

以上より，トルクは「T_H = F_H・D/2」と表すことができます。

📝[memo]　トルクによって流体が動くのであれば「吐出作用」，トルクによって速度差が生じてせん断力を受けるのであれば「微細化作用」が働いていると考えることができます。

仕事

次に，１分間に行う仕事を考えます。

一般に，力が物体に対してした仕事は「力」と「変位」の積で表される量です。

「力＝”流体”に加わる力F_H」と置き換えます。

続いて，「変位」を考えます。

ホモミキサーのような撹拌機は回転するので，回転による移動距離を変位として考えることができます。

「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで紹介した周先端速度πND/60が，１分間あたりの移動距離に相当します。

以上より，１分間に行う仕事は「P_H = F_H・πND/60」と表すことができます。

さらに，トルクT_Hを用いた表現とすると，１分間に行う仕事は「P_H = πT_HN/30」と表すことができます。

📝[memo]　「T_H = F_H・D/2」であったので，「F_H = 2T_H/D」を代入します。

流体が球形粒子に及ぼす抵抗

ホモミキサーを使用してエマルションを調製するとき，生成する乳化粒子は液滴なので球状と言えます。

そこで，撹拌で力を受けた流体が球形粒子に及ぼす抵抗を考えます。

昔，球形粒子の抵抗について次のような実験をした人がいました。

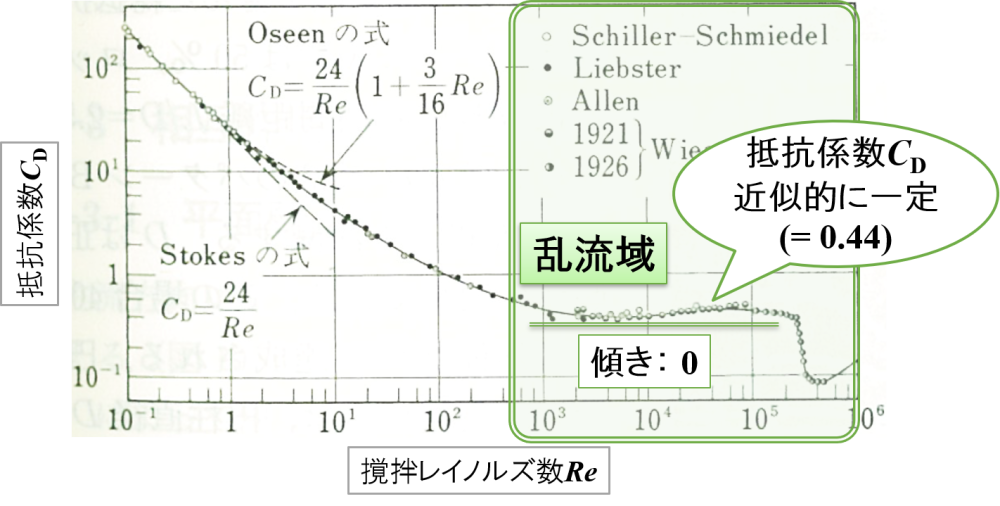
撹拌レイノルズ数Reと抵抗係数C_Dの関係を調べたところ，下図のような傾向があることがわかりました。

「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで紹介したように，通常想定される撹拌機の使用方法であれば，自然と乱流が生じるような撹拌になっていると考えられます。

そこで乱流域に着目すると，グラフの傾きは0とみなすことができます。

すなわち，乱流域では抵抗係数C_Dが近似的に一定となります。

📝[memo]　撹拌レイノルズ数が10⁵以上のときに抵抗係数C_Dが一定とはなっていませんが，ここでは考えないようにします。

引用：Schlichting, H. : Boundary Layer Theory, 6th ed., McGraw-Hill, 1968

そして，球体の抗力実験式が成り立つとして，「”流体”に加わる力F_H」が「球形粒子の抵抗力R_f」と等しくなることを考えます。

「”流体”に加わる力F_H」が「球形粒子の抵抗力R_f」を上回るとき，流体を動かすことができるようになります。

すなわち，流体を動かすために必要な最低限の力と理解することができます。

トルクと仕事

以上の考え方から，撹拌レイノルズ数の違いによってホモミキサーが行う仕事がどうなるかを調べてみたいと思います。

粒子の物性（粘度η・密度ρ・粒子径d）は変化せずに一定であるとします。

乱流 Re > 500

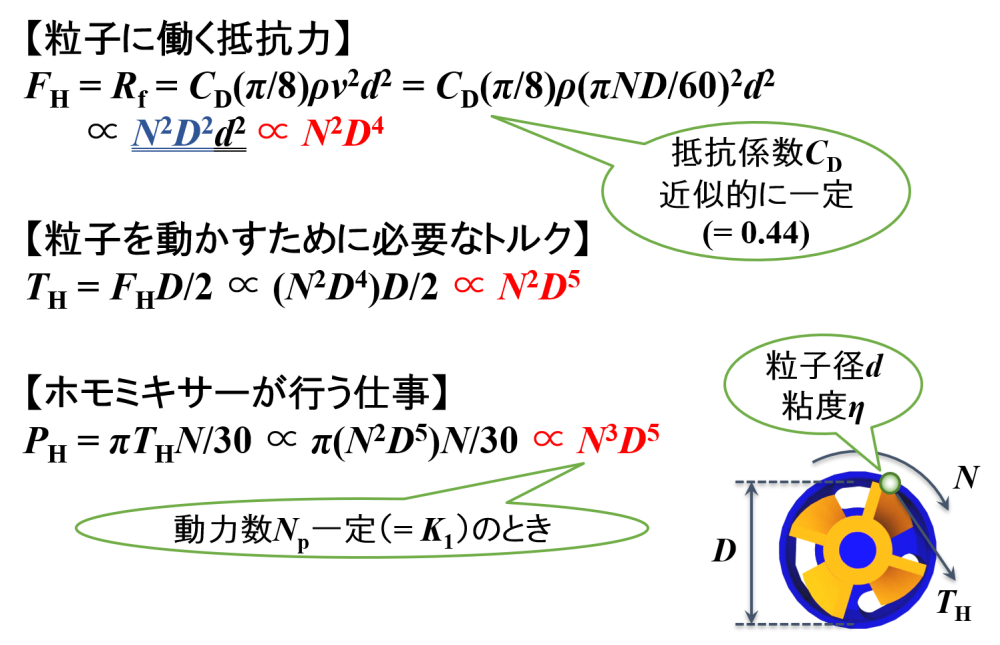
粒子に働く抵抗力

上述した球体の抗力実験式について，抵抗係数C_Dが一定として球形粒子の抵抗力R_fを考えます。

そして，この力と”流体”に加わる力F_Hが等しいとします。

つまり，F_H = R_fが成り立ちます。

続いて，球形粒子の流速vはホモミキサーによる周先端速度U (= πND/60)と等しいとします。

📝[memo]　周先端速度の式は，「スケールアップ理論を考えてみよう ー 乳化編【周先端速度が等しくなるようにする】」のページで紹介しています。

すると，粒子に働く抵抗力は”N²D⁴”に比例することがわかります。

📝[memo]　N → 回転数，D → タービン羽根の直径（羽根径）とします。

📝[memo]　粒子径dは，タービン羽根の直径（羽根径）Dで表現するようにします。

粒子を動かすために必要なトルク

次に，”流体”に加わる力F_Hが”N₂D₄”に比例するとして，粒子を動かすために必要なトルクT_Hを考えます。

上述したホモミキサーによるトルクの式に，F_H = N²D⁴を代入します。

すると，粒子を動かすために必要なトルクは”N²D⁵”に比例することがわかります。

ホモミキサーが行う仕事

最後に，粒子を動かすために必要なトルクT_Hが”N²D⁵”に比例するとして，ホモミキサーが行う仕事P_Hを考えます。

上述したホモミキサーが行う仕事の式，T_H = N²D⁵を代入します。

すると，ホモミキサーが行う仕事は”N³D⁵”に比例することがわかります。

ところで，”N³D⁵”とは何だったでしょうか？

「撹拌をやさしく捉えてみよう【撹拌装置で使用する主な撹拌羽根】」のページで紹介したように，乱流域における正味の所要動力P_netを意味します。

このようにして，「ホモミキサーが行う仕事P_H」と「正味の所要動力P_net」を結びつけることができました。

---

ちなみに，粒子に働く抵抗力は球体の抗力実験式ではなく，Newtonの抵抗則でも表すことができます。

結果的には，上述した同じ結論（”N²D⁴”に比例する）が得られます。

Newtonの抵抗則

F_H = 0.055πρd²v² = 0.055πρd²(πND/60)² ∝ N²D²d² ∝ N²D⁴

層流域 Re < 2

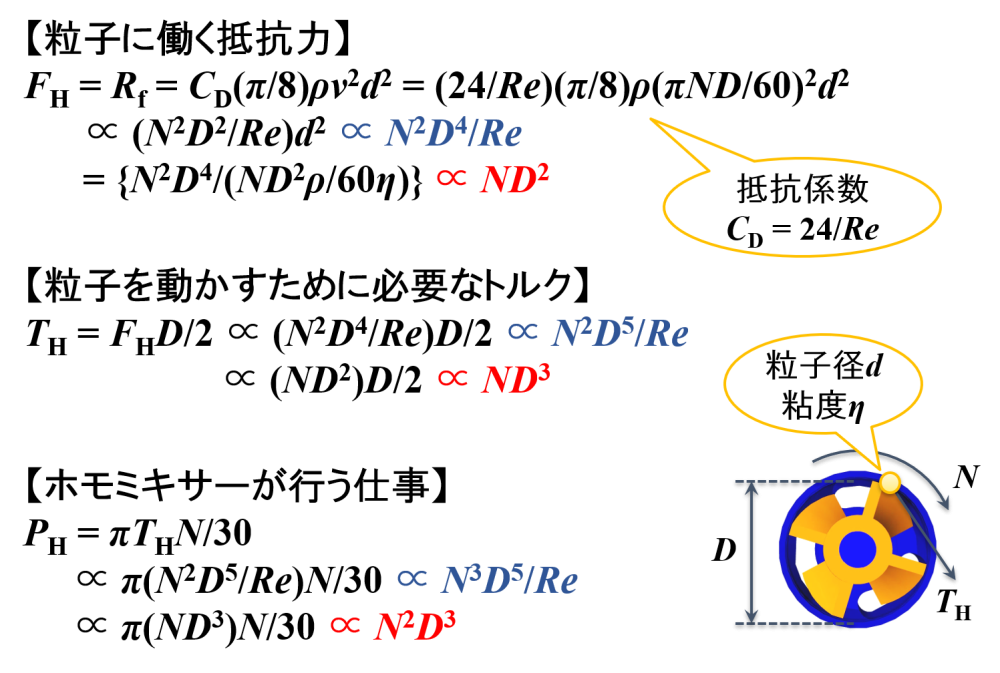
粒子に働く抵抗力

乱流域の場合と同様にして考えます。

層流域の場合，抵抗係数C_D = 24/Reとなります。

📝[memo]　撹拌レイノルズ数は，「撹拌をやさしく捉えてみよう【撹拌による槽内の流動】」のページで紹介しています。

すると，粒子に働く抵抗力は”ND²”に比例することがわかります。

📝[memo]　流体の物性（粘度・密度）を変化させた場合も検討することがあるので，Reを残した式も併記しています。

粒子を動かすために必要なトルク

乱流域の場合と同様にして考えます。

すると，粒子を動かすために必要なトルクは”ND³”に比例することがわかります。

ホモミキサーが行う仕事

乱流域の場合と同様にして考えます。

すると，ホモミキサーが行う仕事は”N²D³”に比例することがわかります。

ところで，”N²D³”とは何でしょうか？

「撹拌をやさしく捉えてみよう【撹拌装置で使用する主な撹拌羽根】」のページで紹介したように，層流域における正味の所要動力Pnetを意味します。

このようにして，「ホモミキサーが行う仕事P_H」と「正味の所要動力P_net」を結びつけることができました。

---

参考までに，粒子に働く抵抗力について，Stokesの抵抗則を導入することを考えます。

これは，「スケールアップでエマルションを評価しよう【エマルションの安定性（クリーミング）】」のページで紹介したStokesの式の考え方で登場するものです。

次の条件を満たすとすると，”ND²”に比例することがわかります。

• 粒子が球であるとき
• 球の速度vが極めて遅く，粘性力が支配するとき

Stokesの抵抗則

F_H = 3πηdv = 3πηd(πND/60) ∝ NDd ∝ ND²

乱流域における粘度・周先端速度変化

層流域の場合では抵抗係数C_D = 24/Reとなるので，ホモミキサーが行う仕事を表す際にReを残した式も併記しました。

一方で，乱流域の場合ではReを残した式を併記することはありませんでした。

📝[memo]　抵抗係数が近似的に一定としたため，撹拌レイノルズ数が出てきませんでした。

しかしながら，特に流体の粘度を変化させた場合も検討することがあるかと思います。

例えば，同じ条件で粘度が異なる流体を撹拌するような場合，ホモミキサーが行う仕事から撹拌機が使用できるか否かを調べたいときです。

そのため，撹拌レイノルズ数と抵抗係数の詳細な関係が知りたくなります。

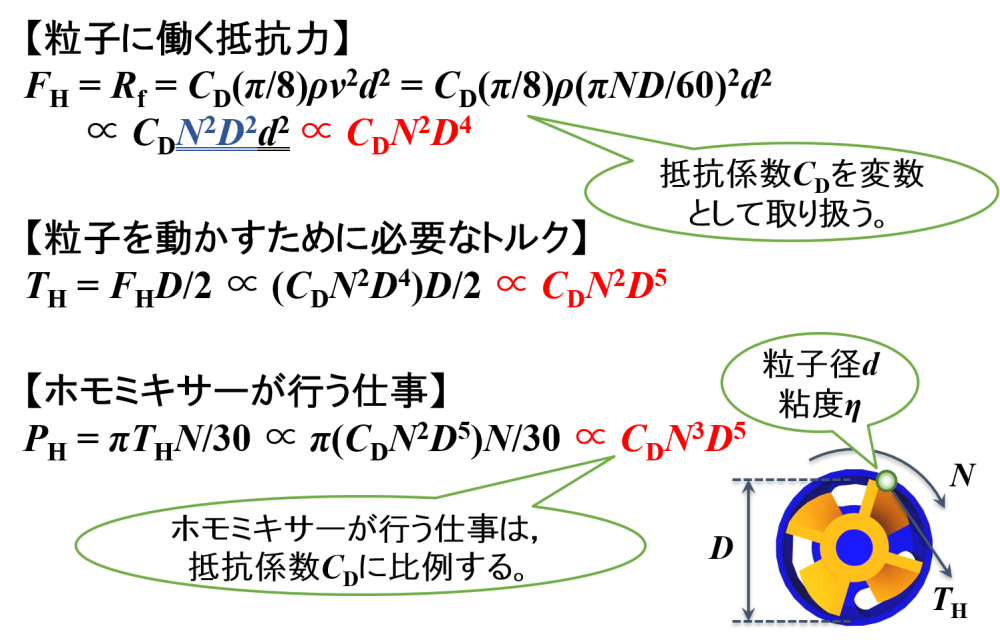
抵抗係数CDを変数として取り扱うとき

抵抗係数が一定ではなく，変数として取り扱った場合を考えます。

ホモミキサーが行う仕事は”N³D⁵”に比例することに間違いありませんが，さらに抵抗係数にも比例することがわかります。

撹拌レイノルズ数と抵抗係数の関係

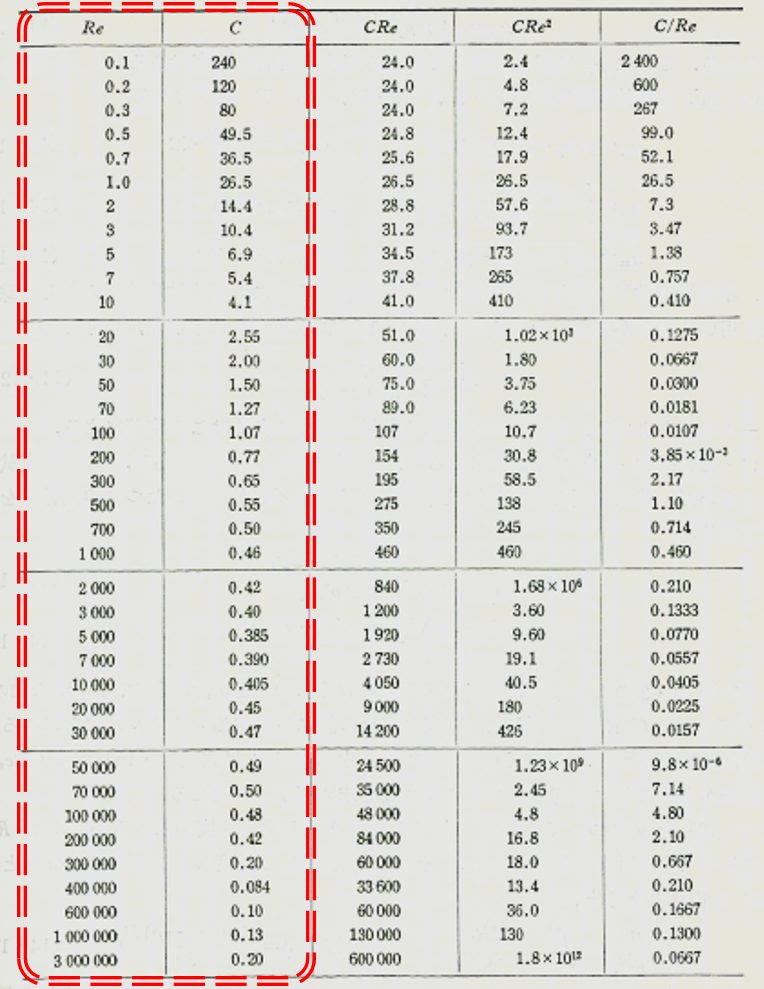
ここでは，文献にて撹拌レイノルズ数と抵抗係数の関係を紹介します。

乱流域について議論しているので、撹拌レイノルズ数が700以上のときに注目したいと思います。

📝[memo]　表中のCが，抵抗係数C_Dに相当します。

例えば，ある撹拌条件で製品を撹拌することを想定したとき，撹拌レイノルズ数は「Re₁ = 300,000」だったとします。

このときの抵抗係数は「C_D1 = 0.20」です。

そして，撹拌条件は同じで粘度が100倍になった製品を撹拌することを考えます。
すると撹拌レイノルズ数は「Re₂ = 3000」となり，このときの抵抗係数は「C_D2 = 0.40」です。

📝[memo]　粘度が100倍になると，撹拌レイノルズ数は1/100になります。

その結果，C_D2/C_D1 = 0.40/0.20 = 2倍の動力が必要になることが予想されます。

引用：Lapple, C. E. and C. B. Shepherd: Ind. Eng. Chem., 32. 605 (1940)
Perry, R. H., et al.: “Chemical Engineers’ Handbook”, 4th ed., 5-61. McGraw-Hill, New York (1963)

ただし，これはあくまでも推測値であり考え方の一例です。

製品の粘度が変わったとしても，ホモミキサーが行う仕事が同じように発揮されていることが前提です。

撹拌機メーカーが持つノウハウや経験を加味して，最終的な判断がなされます。